Mathematics
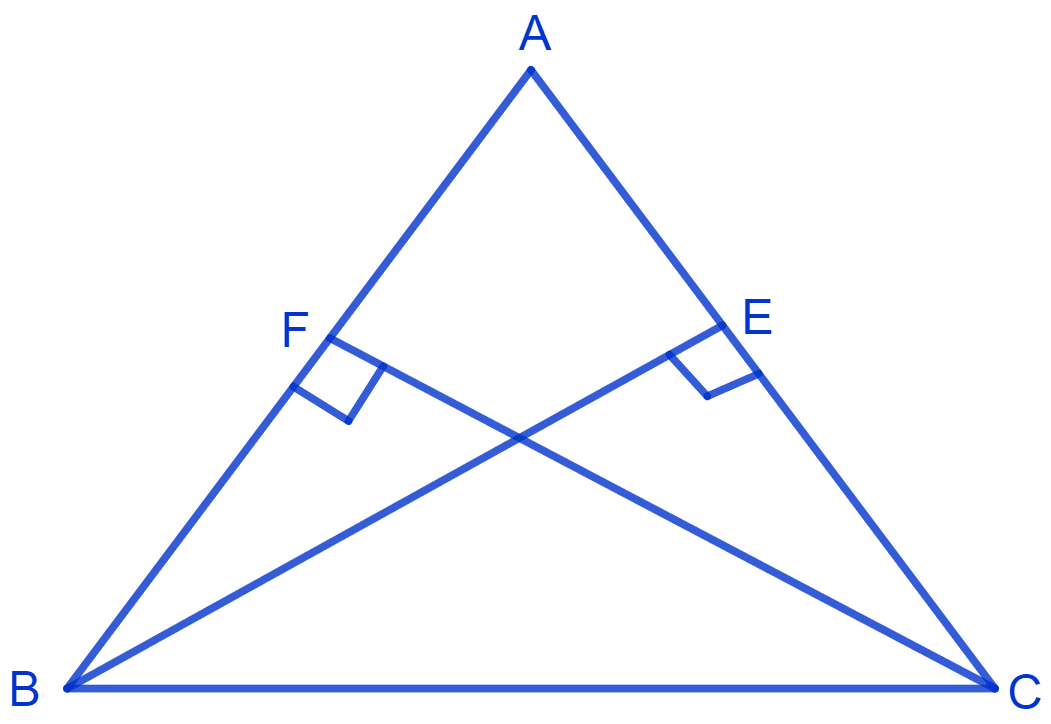
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal. Show that
(i) Δ ABE ≅ Δ ACF
(ii) AB = AC, i.e., ABC is an isosceles triangle
Triangles
30 Likes
Answer
Given :
BE = CF, where BE and CF are altitudes
So, ∠AEB = 90° and ∠AFC = 90°
(i) In Δ ABE and Δ ACF,
⇒ ∠AEB = ∠AFC (Each 90°)
⇒ ∠A = ∠A (Common angle)
⇒ BE = CF (Given)
∴ Δ ABE ≅ Δ ACF (By A.A.S. congruence rule)
Hence, proved that Δ ABE ≅ Δ ACF.
(ii) As,
Δ ABE ≅ Δ ACF
We know that,
Corresponding parts of congruent triangles are equal.
∴ AB = AC (By C.P.C.T.)
Hence, proved that ABC is an isosceles triangle with AB = AC.
Answered By
18 Likes
Related Questions
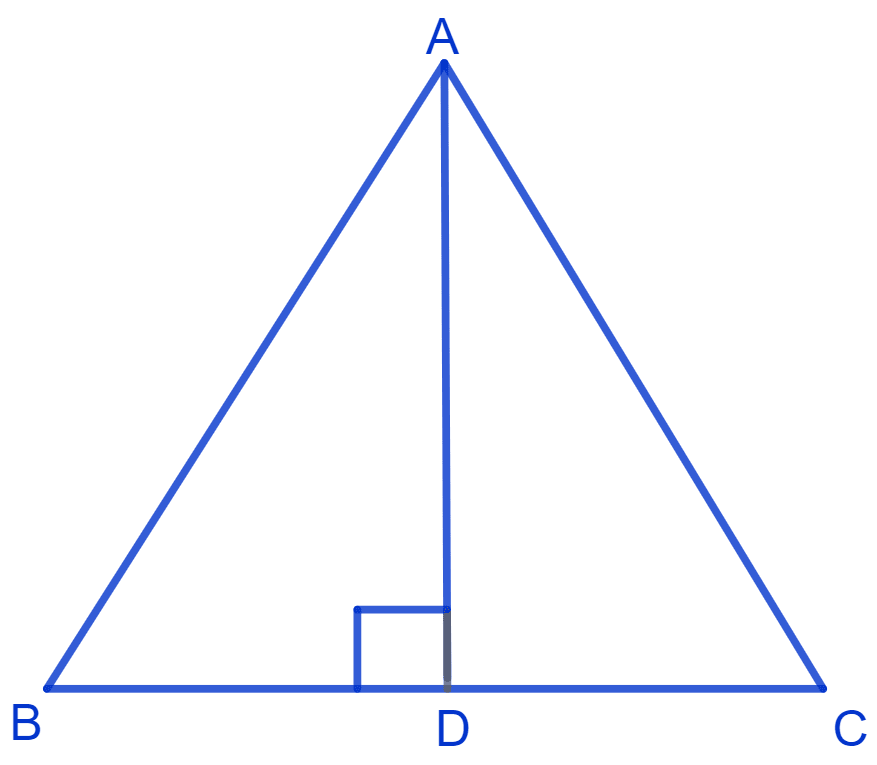
In Δ ABC, AD is the perpendicular bisector of BC. Show that Δ ABC is an isosceles triangle in which AB = AC.
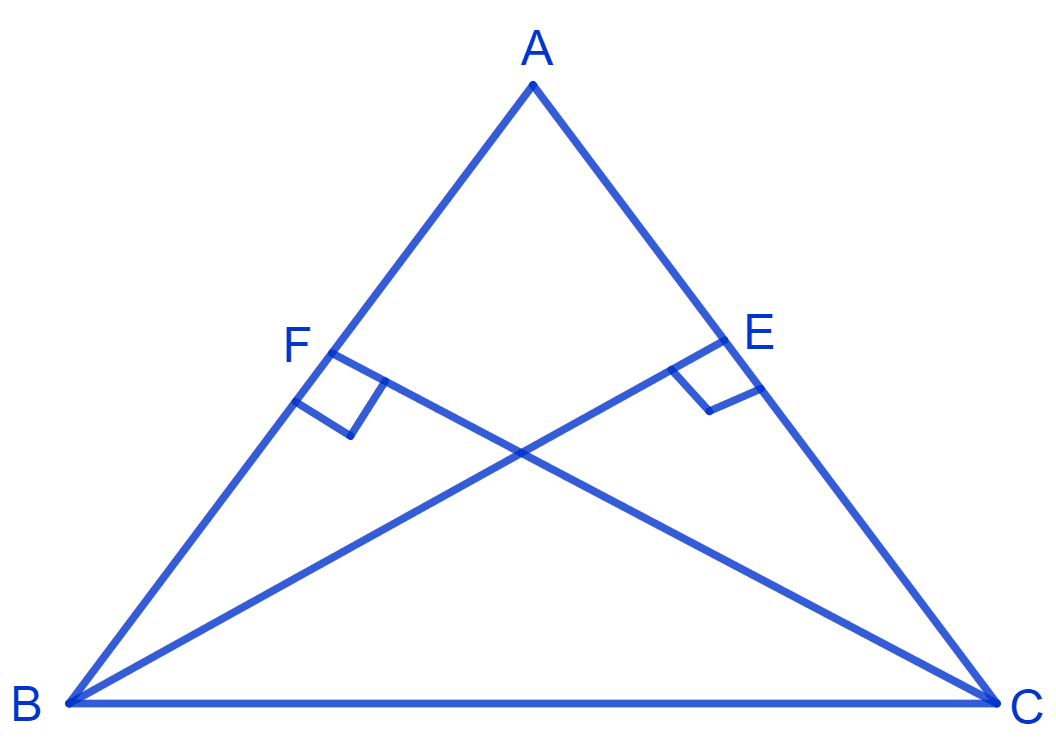
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively see Fig. Show that these altitudes are equal.
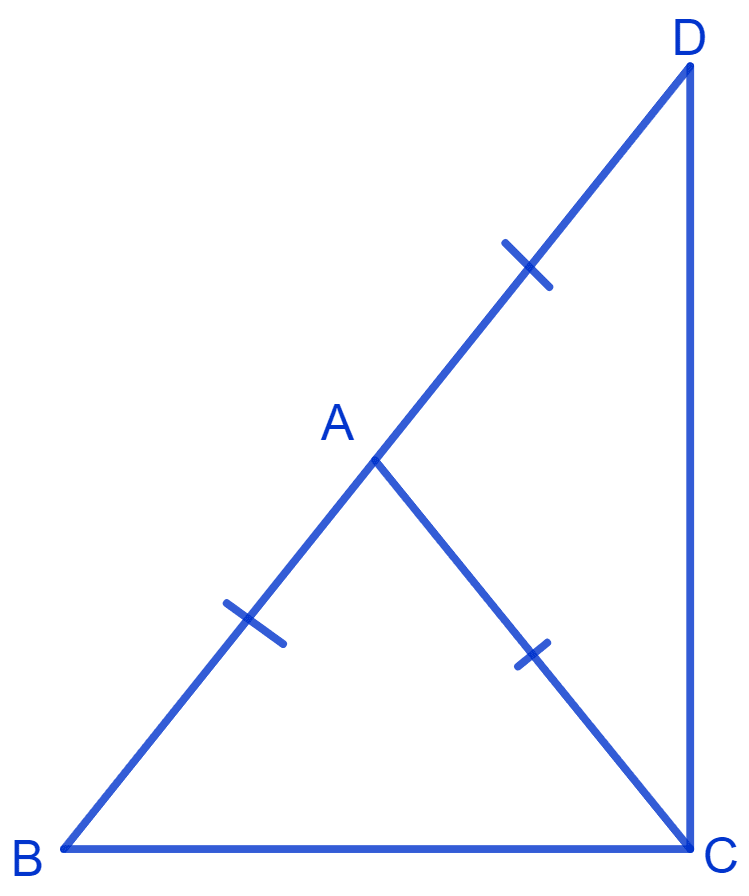
ABC and DBC are two isosceles triangles on the same base BC. Show that ∠ABD = ∠ACD.
Δ ABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB. Show that ∠BCD is a right angle.