Mathematics
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA =
Rectilinear Figures
21 Likes
Answer
(i) In Δ ABC,
It is given that M is the mid-point of AB and MD || BC.

By converse of mid-point theorem, we get :
Thus, D is the mid-point of AC.
Hence, proved that D is the mid-point of AC.
(ii) As DM || CB and AC is a transversal,
We know that,
Sum of co-interior angles = 180°.
⇒ ∠MDC + ∠DCB = 180°
⇒ ∠MDC + 90° = 180°
⇒ ∠MDC = 180° - 90°
⇒ ∠MDC = 90°
Hence, proved that MD ⊥ AC.
(iii) Join MC,
In Δ AMD and Δ CMD,
⇒ AD = CD (D is the mid-point of side AC)
⇒ ∠ADM = ∠CDM (Since, MD ⊥ AC)
⇒ DM = DM (Common side)
∴ Δ AMD ≅ Δ CMD (By S.A.S. congruence rule)
We know that,
Corresponding parts of congruent triangles are equal.
⇒ AM = CM (By C.P.C.T.)
We know that,
M is the mid-point of AB.
∴ AM =
⇒ CM = AM = .
Hence, proved that CM = MA = .
Answered By
7 Likes
Related Questions
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
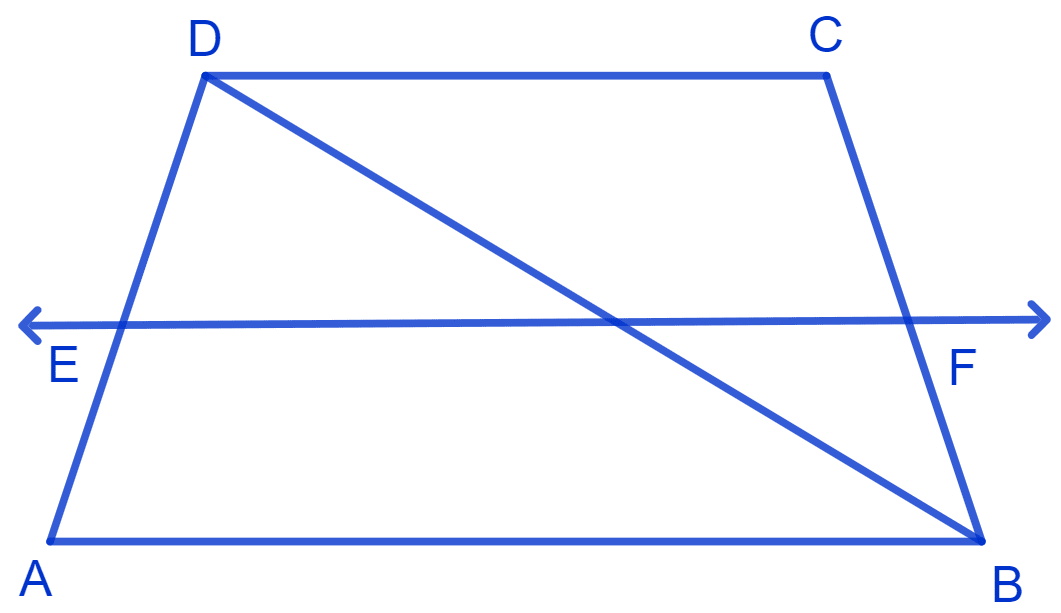
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F see Fig. Show that F is the mid-point of BC.
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively see Fig. Show that the line segments AF and EC trisect the diagonal BD.