Mathematics
In ΔABC, PQ is perpendicular bisector of side AB and PR is perpendicular bisector of side BC.
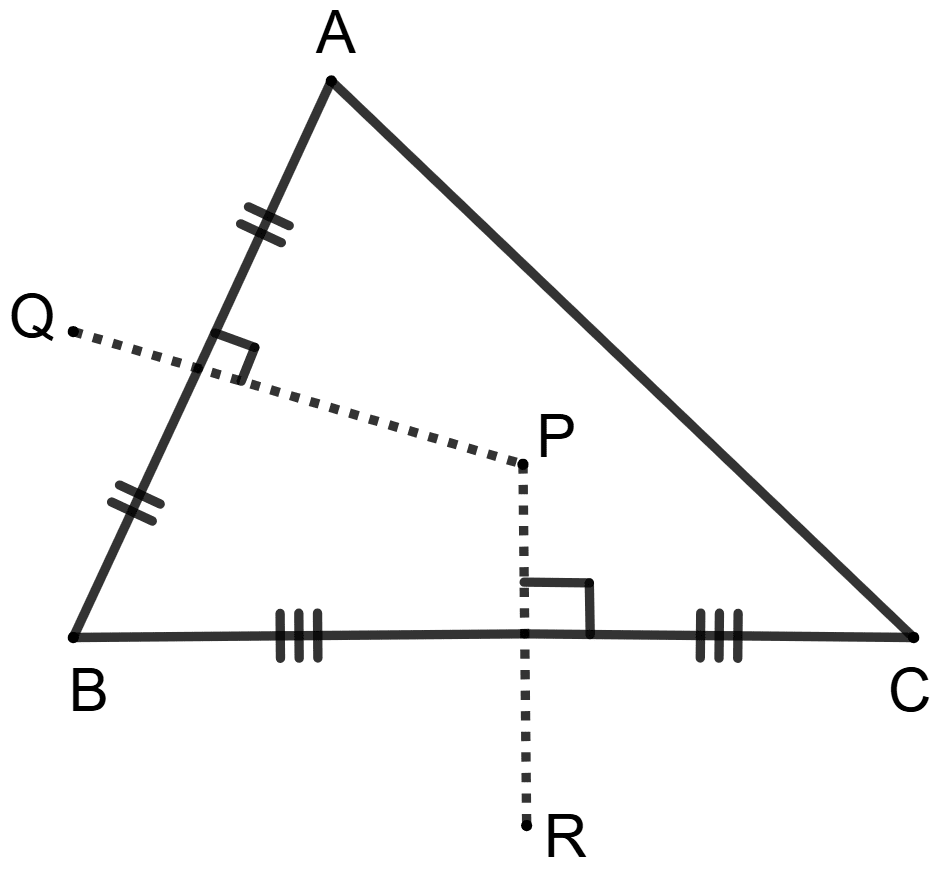
Statement (1): Perpendicular bisector of side AC will pass through point P.
Statement (2): Perpendicular bisectors of sides of a triangle are concurrent.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Constructions
2 Likes
Answer
Since PQ is the perpendicular bisector of AB, any point on PQ is equidistant from A and B.
Similarly, since PR is the perpendicular bisector of BC, any point on PR is equidistant from B and C.
Therefore, point P, which lies on both PQ and PR, is equidistant from A, B and C.
This means that P is the center of a circle passing through A, B and C.
The perpendicular bisectors for sides AB, BC, and CA always meet at a single point called the circumcenter of ∆ ABC that is equidistant from all three vertices.
Thus, we can say that,
Perpendicular bisectors of sides of a triangle are concurrent.
So, statement 2 is true.
Consequently, the perpendicular bisector of AC must also pass through P, as P is equidistant from A and C.
So, statement 1 is true.
∴ Both the statements are true.
Hence, option 1 is the correct option.
Answered By
3 Likes
Related Questions
In triangle ABC, bisectors of angles A and B meet at point P.
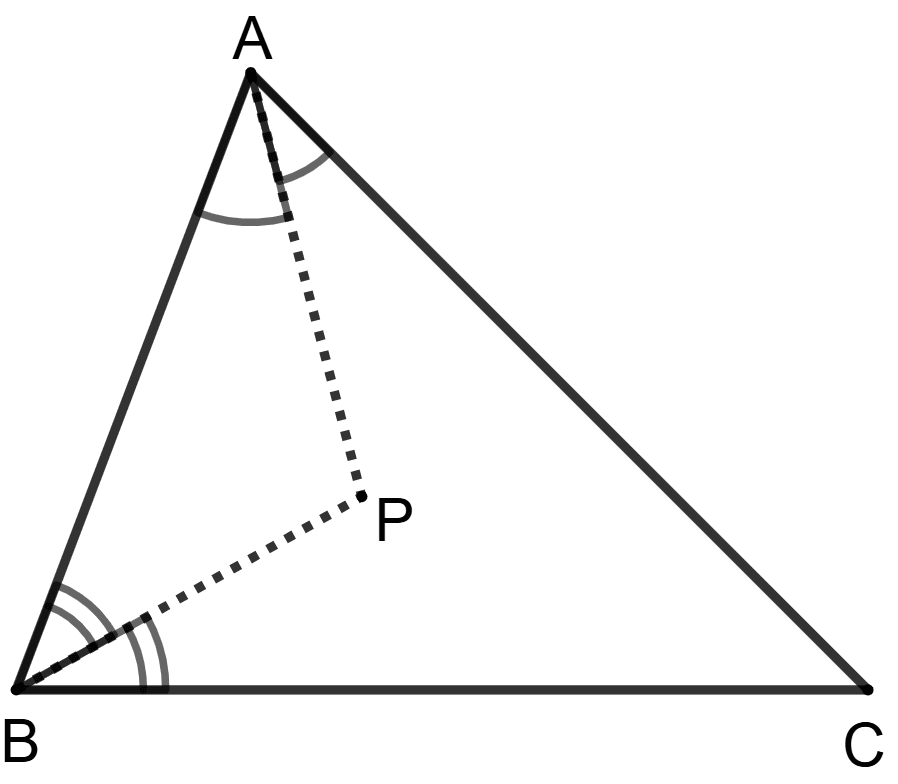
Assertion (A): PC bisects angle C.
Reason(R): Bisectors of angles of a triangle are concurrent.
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.
In triangle ABC, ∠A = 35° and ∠C = 55°.
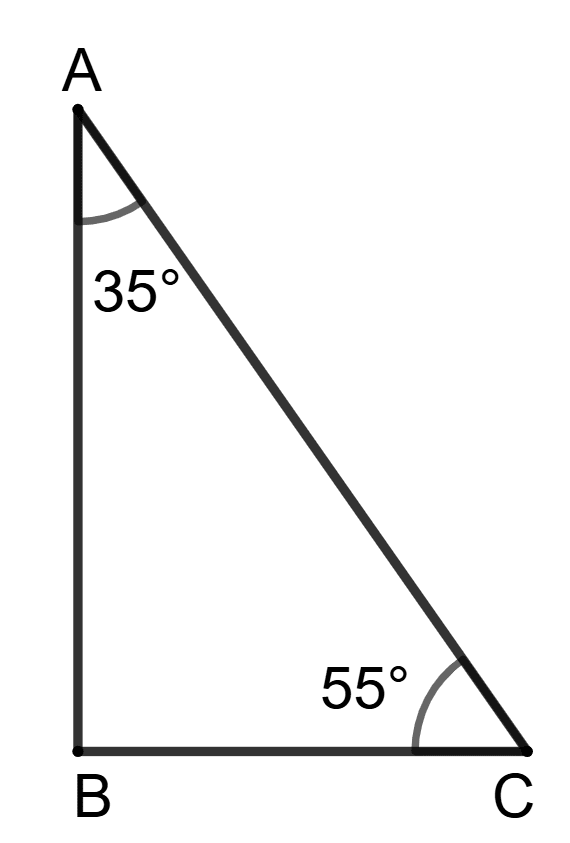
Assertion (A): Circle with AC as diameter will pass through the vertex B.
Reason(R): ∠ABC = 180° - (35° + 55°) = 90° = angle of semi-circle.
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.
Pentagon ABCDE is inscribed in a circle with center O.
Statement (1): ∠AOB =
Statement (2): If pentagon is regular, ∠AOB =
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Draw a circle of radius 3 cm. Mark a point P at a distance of 5 cm from the center of the circle drawn. Draw two tangents PA and PB to the given circle and measure the length of each tangent.