Mathematics
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC
(ii) AD bisects ∠A
Triangles
10 Likes
Answer
Given :
Δ ABC is an isosceles triangle and AB = AC.
AD is altitude
∴ ∠ADB = ∠ADC = 90°.
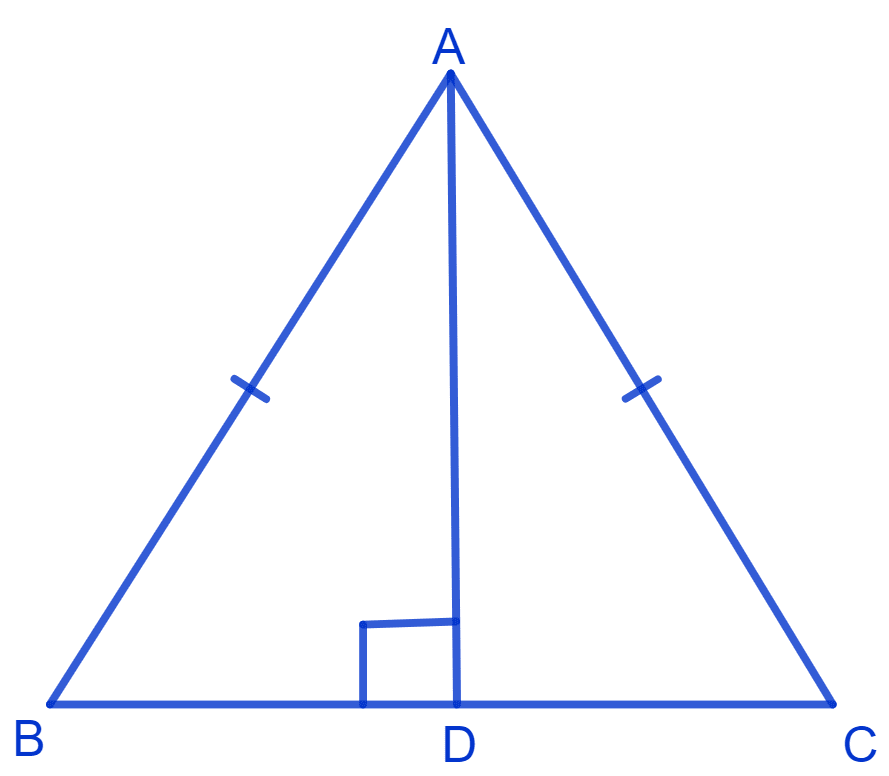
(i) In Δ BAD and Δ CAD,
⇒ ∠ADB = ∠ADC (Each equal to 90° as AD is altitude)
⇒ AB = AC (Given)
⇒ AD = AD (Common)
∴ Δ BAD ≅ Δ CAD (By R.H.S. Congruence rule)
We know that,
Corresponding parts of congruent triangles are equal.
∴ BD = CD (By C.P.C.T.)
Hence, proved that AD bisects BC.
(ii) Since, Δ BAD ≅ Δ CAD
∴ ∠BAD = ∠CAD (By C.P.C.T.)
Hence, proved that AD bisects ∠A.
Answered By
6 Likes
Related Questions
Show that the angles of an equilateral triangle are 60° each.
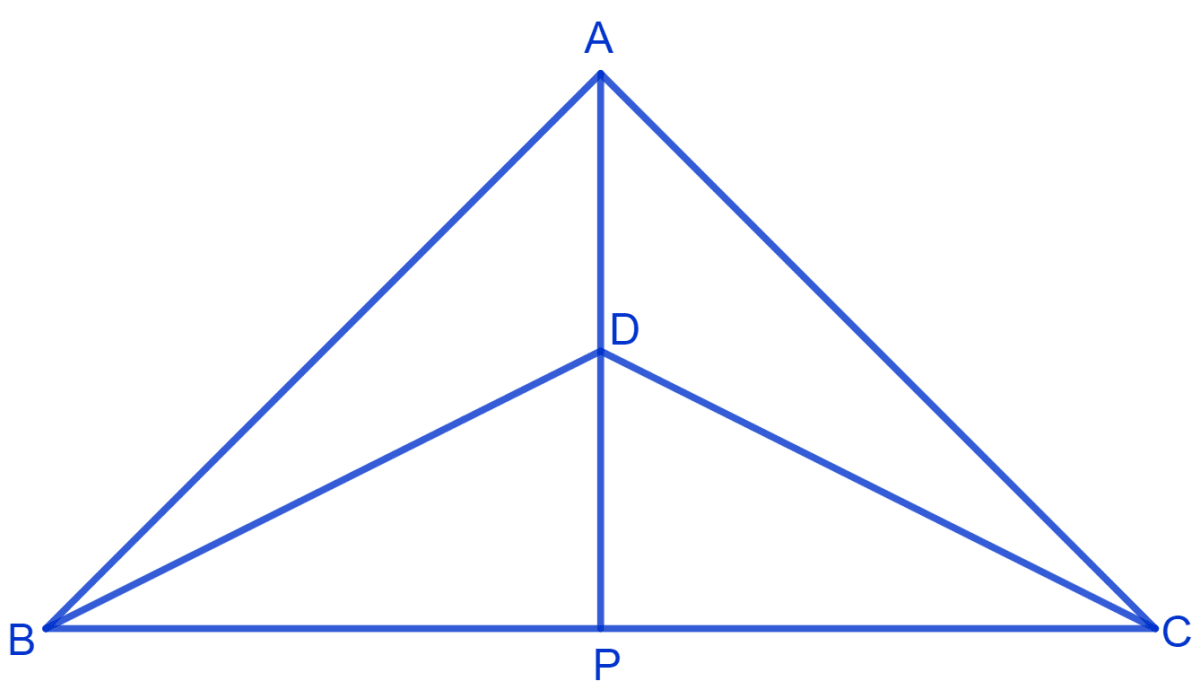
Δ ABC and Δ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that
(i) Δ ABD ≅ Δ ACD
(ii) Δ ABP ≅ Δ ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC
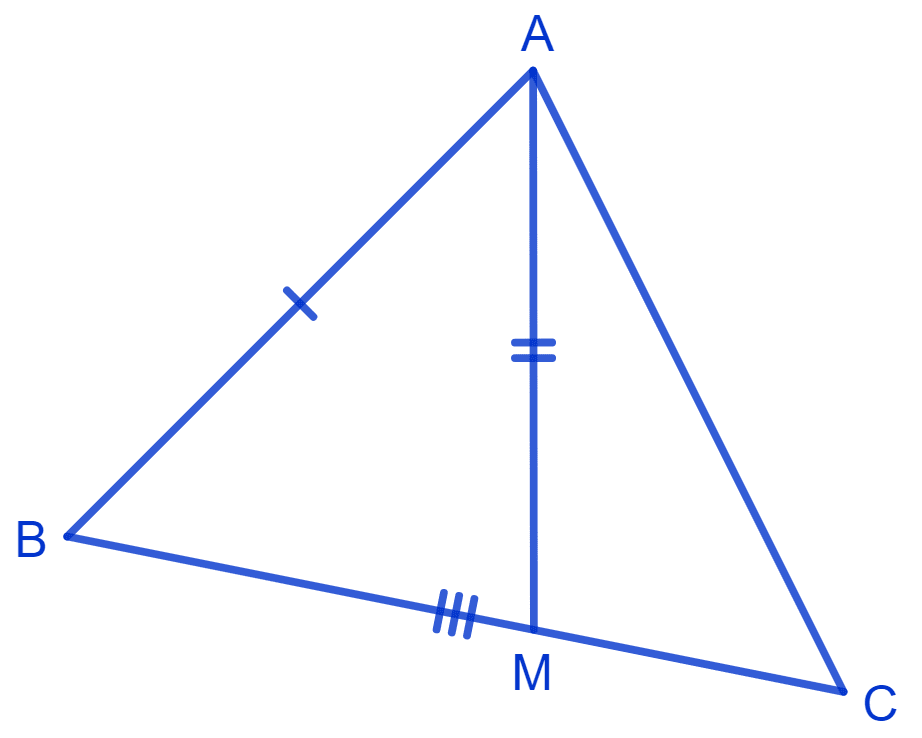
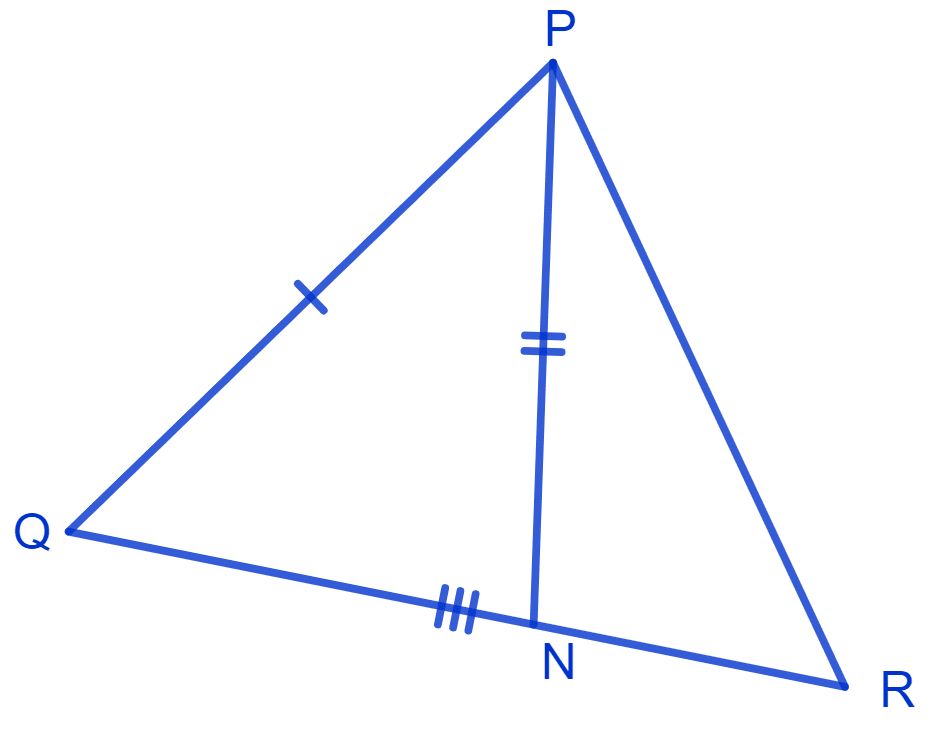
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of Δ PQR. Show that :
(i) Δ ABM ≅ Δ PQN
(ii) Δ ABC ≅ Δ PQR
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.