Mathematics
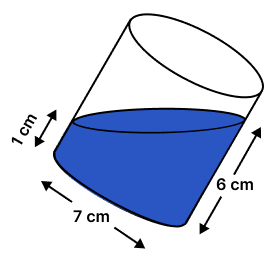
In the adjoining diagram, a tilted right circular cylindrical vessel with base diameter 7 cm contains a liquid. When placed vertically, the height of the liquid in the vessel is the mean of two heights shown in the diagram. Find the area of wet surface, when the cylinder is placed vertically on a horizontal surface. (Use )
Mensuration
ICSE Sp 2025
93 Likes
Answer
When vertically placed,
Height of liquid (h) = cm
Diameter of base = 7 cm
Radius (r) = cm
Hence, area of wet surface = 115.5 cm2.
Answered By
53 Likes
Related Questions
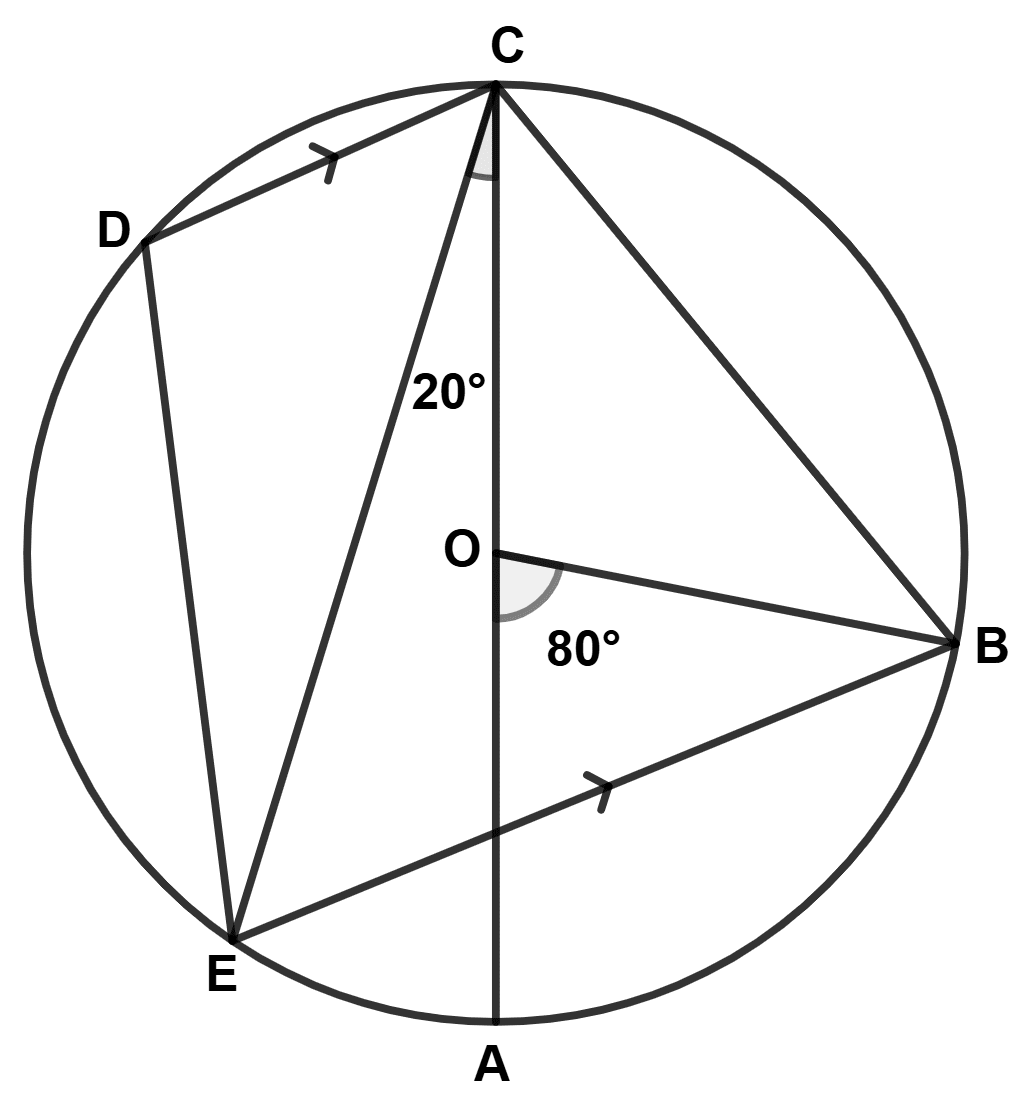
In the given figure AC is the diameter of the circle with center O. CD is parallel to BE.
∠AOB = 80° and ∠ACE = 20°. Calculate :
(a) ∠BEC
(b) ∠BCD
(c) ∠CED
In a Geometric Progression (G.P.) the first term is 24 and the fifth term is 8. Find the ninth term of the G.P.
Study the graph and answer each of the following :
(a) Write the coordinates of points A, B, C and D.
(b) Given that, point C is the image of point A. Name and write the equation of the line of reflection.
(c) Write the coordinates of the image of the point D under reflection in y-axis.
(d) What is the name given to a point whose image is the point itself ?
(e) On joining the points A, B, C, D and A in order, a figure is formed. Name the closed figure.
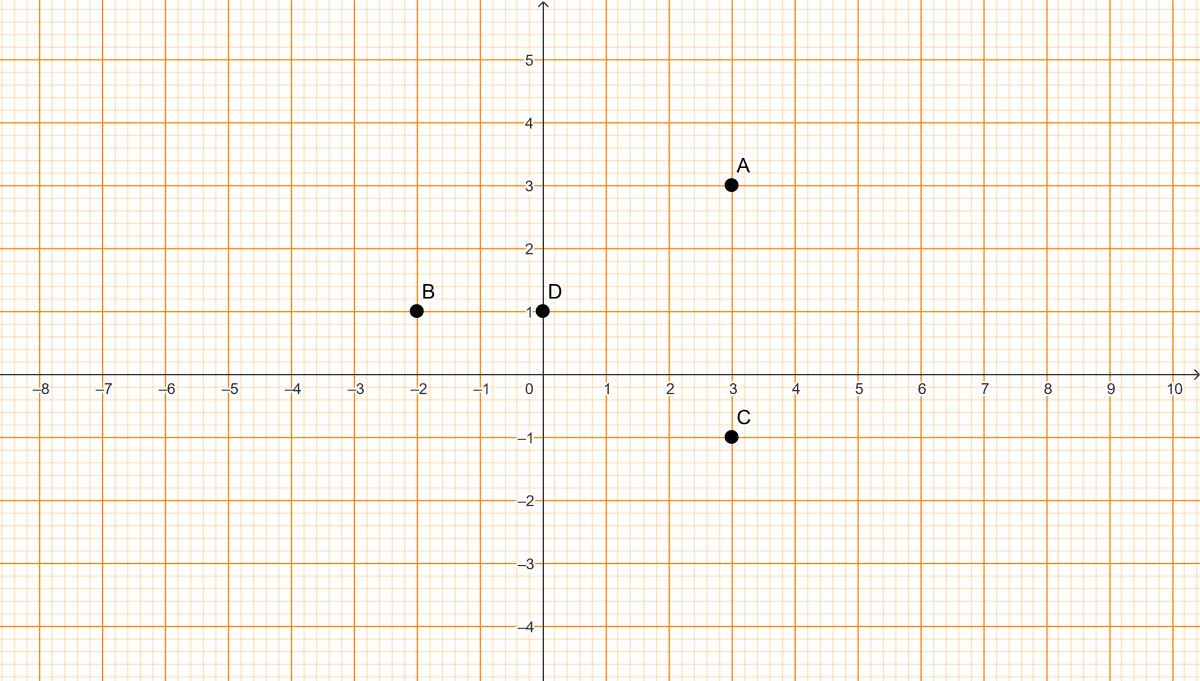
A man buys 250, ten-rupee shares each at ₹12.50. If the rate of dividend is 7%, find the :
(a) dividend he receives annually.
(b) percentage return on his investment.