Mathematics
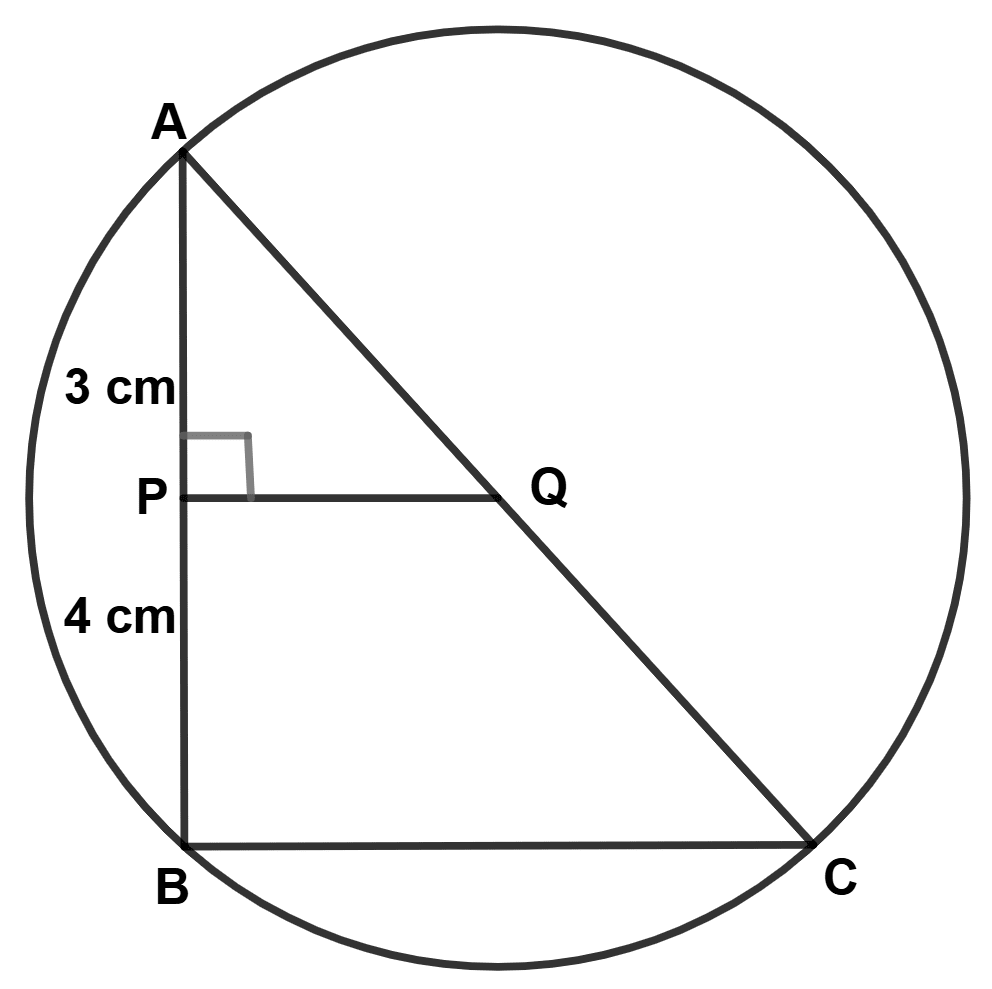
In the adjoining figure, AC is a diameter of the circle, AP = 3 cm and PB = 4 cm and QP ⊥ AB. If the area of △ APQ is 18 cm2, then the area of shaded portion QPBC is :
32 cm2
49 cm2
80 cm2
98 cm2
Circles
ICSE Sp 2025
118 Likes
Answer
We know that,
Angle in a semi-circle is a right angle.
∴ ∠ABC = 90°.
In △ APQ and △ ABC,
⇒ ∠APQ = ∠ABC (Both equal to 90°)
⇒ ∠PAQ = ∠BAC (Common angles)
∴ △ APQ ~ △ ABC (By A.A. axiom)
We know that,
The ratio of area of similar triangles is equal to the ratio of the square of the corresponding sides.
From figure,
Area of QPBC = Area of △ ABC - Area of △ APQ = 98 - 18 = 80 cm2.
Hence, Option 3 is the correct option.
Answered By
76 Likes
Related Questions
A polynomial in 'x' is divided by (x - a) and for (x - a) to be a factor of this polynomial, the remainder should be :
-a
0
a
2a
Radha deposited ₹ 400 per month in a recurring deposit account for 18 months. The qualifying sum of money for the calculation of interest is :
₹ 3600
₹ 7200
₹ 68,400
₹ 1,36,800
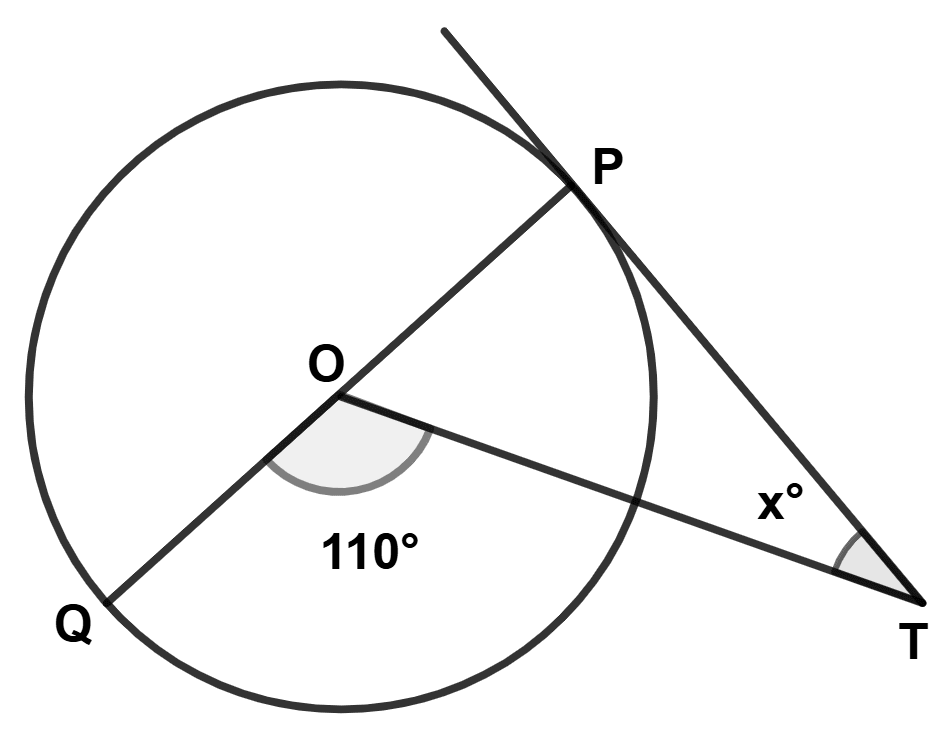
In the adjoining diagram, O is the center of the circle and PT is a tangent. The value of x is :
20°
40°
55°
70°
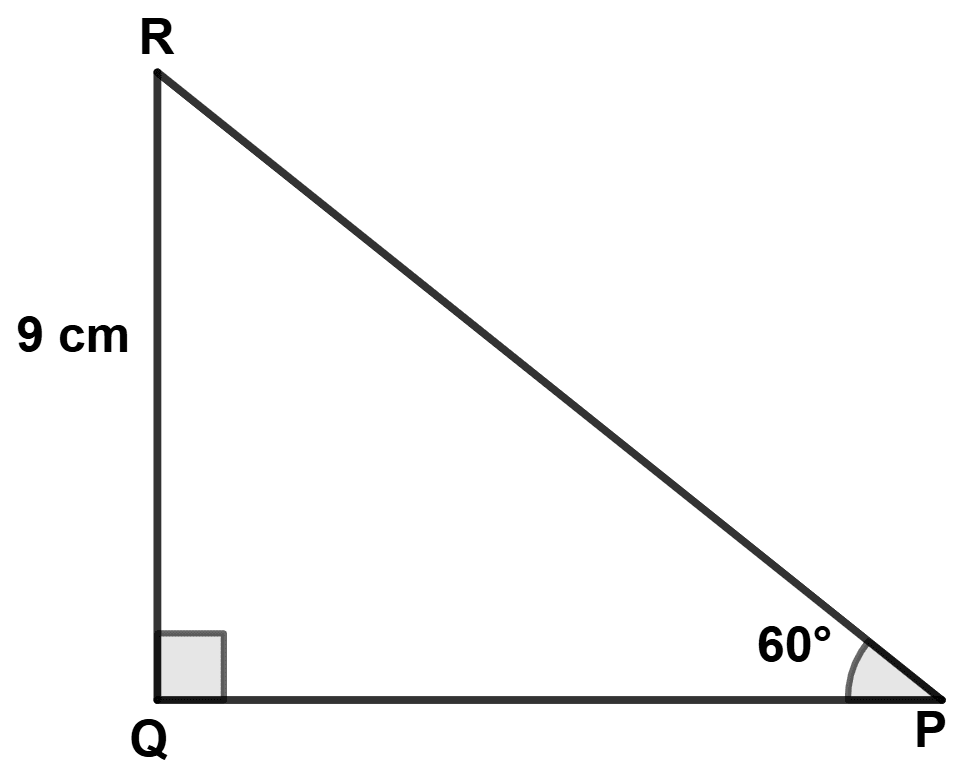
In the adjoining diagram the length of PR is :
cm
cm
cm
18 cm