Mathematics
In adjoining figure, P and Q are the centers of two circles touching externally at R and CD is the common tangent.
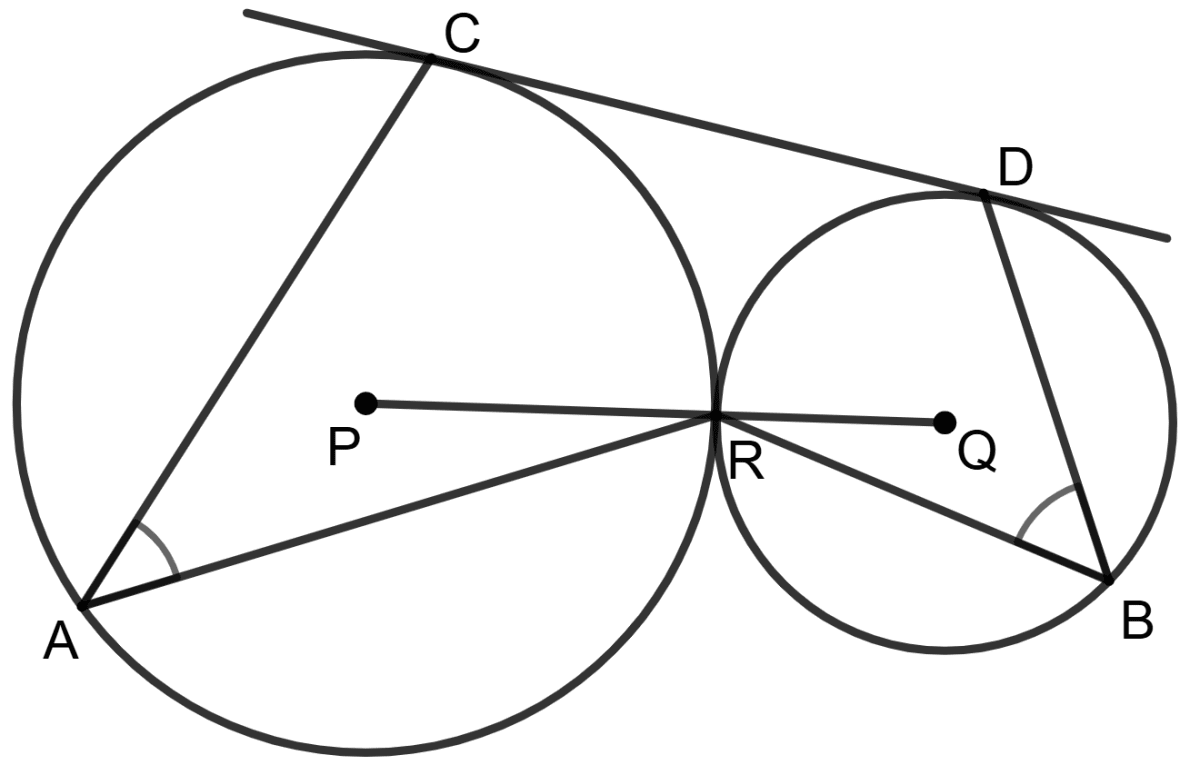
If ∠CAR = 38°, then find ∠DBR.
Circles
9 Likes
Answer
Join PC and QD.
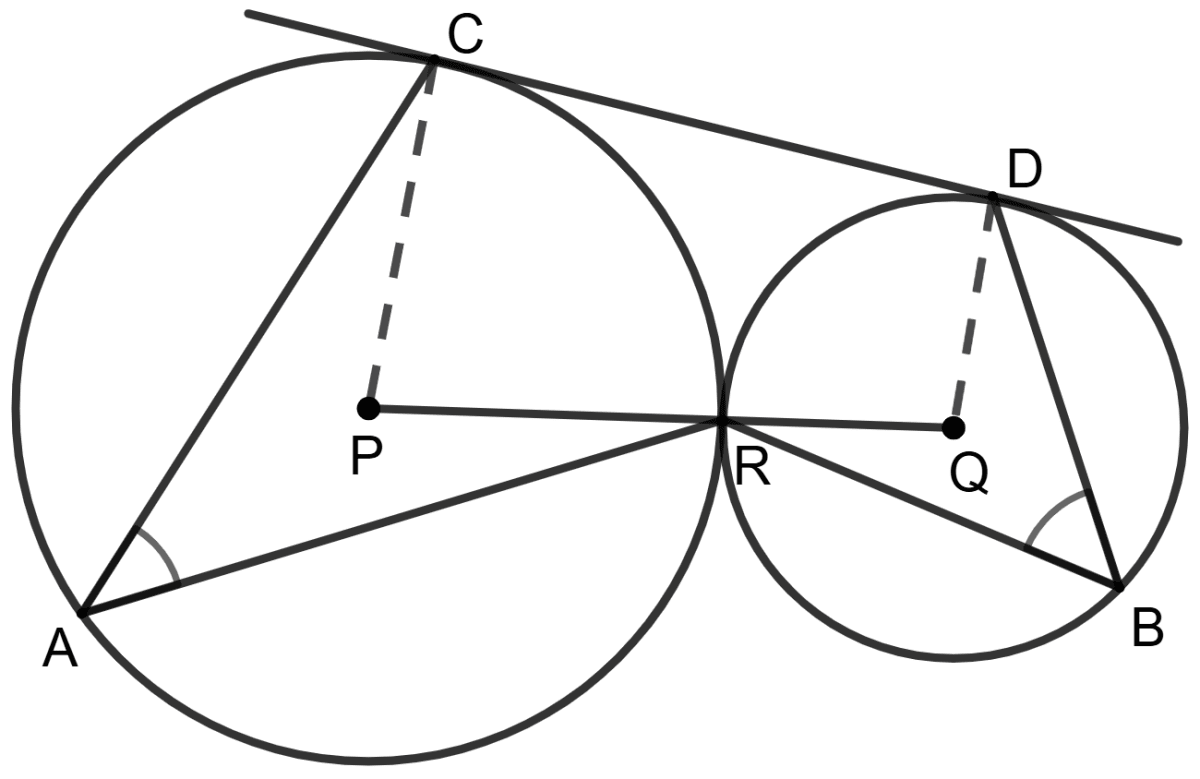
We know that,
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ PC ⊥ CD and QD ⊥ CD
⇒ ∠PCD = 90° and ∠QDC = 90°
The angle subtended by an arc of a circle at the center is double the angle subtended by it at any point on the remaining part of the circle.
⇒ ∠CPR = 2 x ∠CAR = 2 x 38° = 76°
⇒ ∠CPR = ∠CPQ = 76°
CDQP is quadrilateral.
∴ ∠PCD + ∠QDC + ∠DQP + ∠CPQ = 360°
⇒ 90° + 90° + ∠DQP + 76° = 360°
⇒ 256° + ∠DQP = 360°
⇒ ∠DQP = 360° - 256°
⇒ ∠DQP = 104°
From figure,
⇒ ∠DQR = ∠DQP
⇒ ∠DQR = 104°
The angle subtended by an arc of a circle at the center is double the angle subtended by it at any point on the remaining part of the circle.
⇒ ∠DQR = 2 x ∠DBR
⇒ 104° = 2 x ∠DBR
⇒ ∠DBR =
⇒ ∠DBR = 52°.
Hence, ∠DBR = 52°.
Answered By
4 Likes
Related Questions
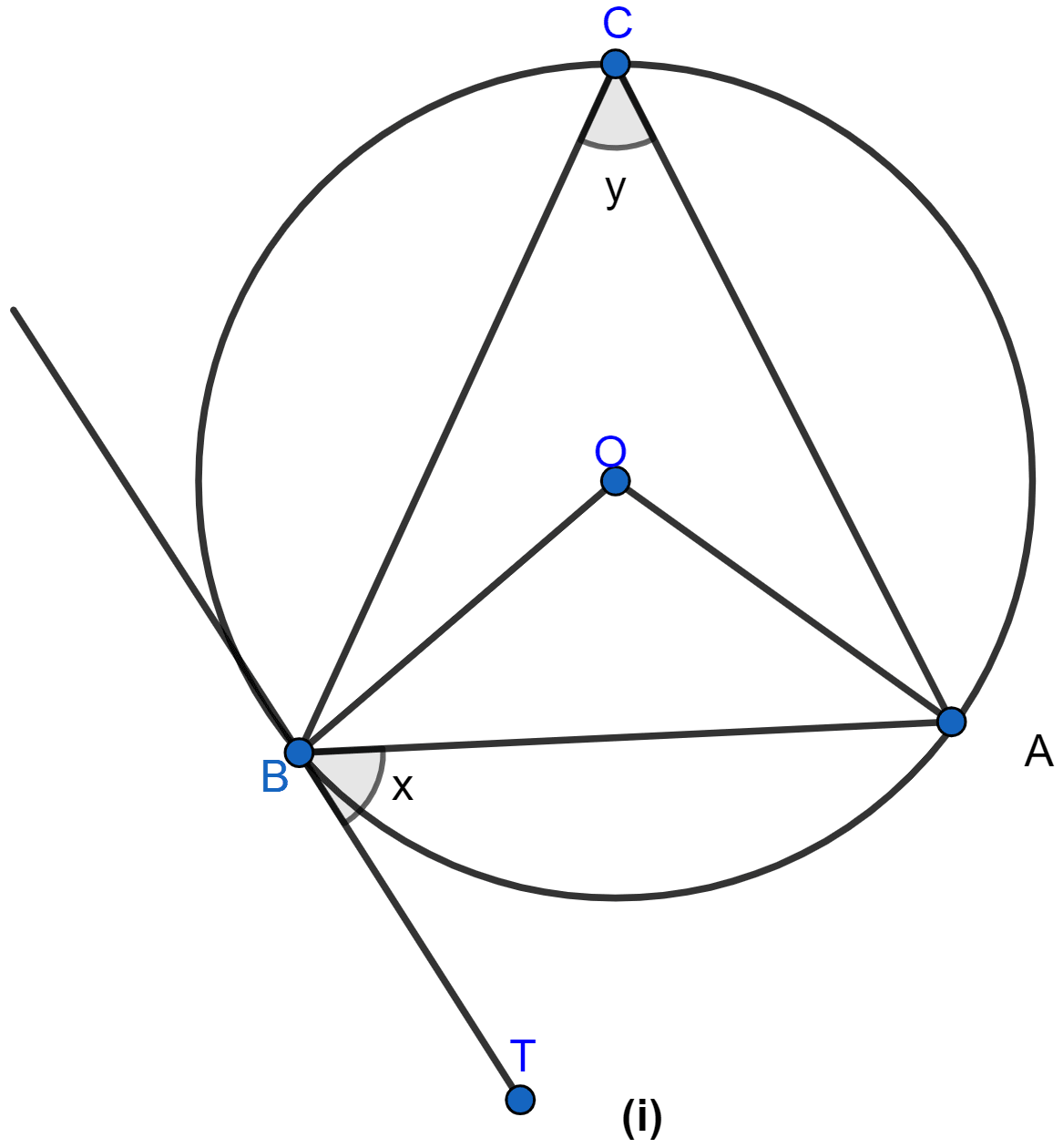
In the figure (i) given below, AB is a chord of the circle with centre O, BT is tangent to the circle. If ∠OAB = 32°, find the values of x and y.
In the figure (ii) given below, O and O' are centres of two circles touching each other externally at the point P. The common tangent at P meets a direct common tangent AB at M. Prove that,
(i) M bisects AB.
(ii) ∠APB = 90°.

In the adjoining figure, O is the centre of the circle. If ∠OAB = 40°, then ∠ACB is equal to
50°
40°
60°
70°

ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140°, then ∠BAC is equal to
80°
50°
40°
30°