An exhibition tent is in the form of a cylinder surmounted by a cone. The height of the tent above the ground is 85 m and the height of the cylindrical part is 50 m. If the diameter of the base is 168 m, find the quantity of canvas required to make the tent. Allow 20% extra for folds and stitching. Give your answers to the nearest m².

Total height of the tent = 85 m.

Height of the cylindrical part (h₁) = 50 m.

From figure,

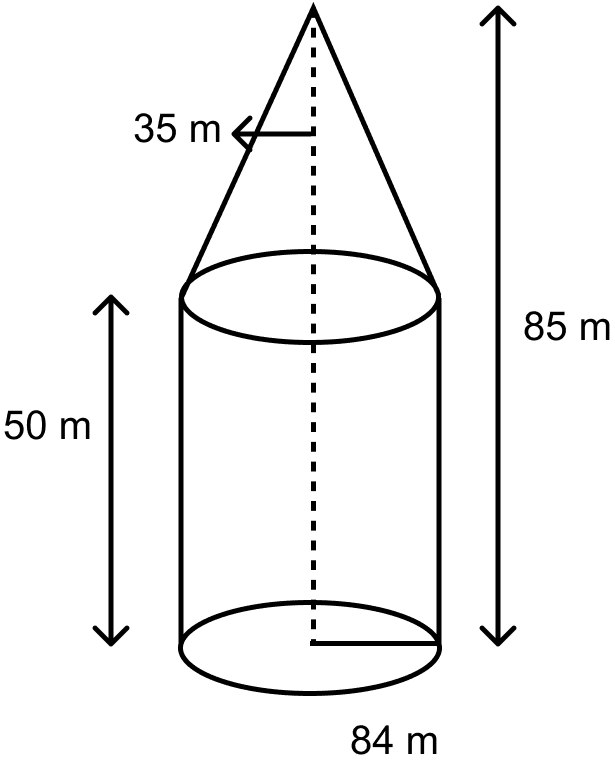
Height of cone (h₂) = 85 - 50 = 35 m.

Diameter of the base, d = 168 m.

Radius of the base of cylindrical part, r = $\dfrac{d}{2} = \dfrac{168}{2} = 84$ m.

Slant height of the cone, l = $\sqrt{h^2 + r^2}$.

l = $\sqrt{35^2 + 84^2} = \sqrt{1225 + 7056} = \sqrt{8281} = 91$ m.

Surface area of tent (S) = Curved surface area of cylinder + Curved surface area of cone

Putting values we get,

$S = 2πrh$1 + πrl \\[1em] = πr(2h1 + l) \\[1em] = \dfrac{22}{7} \times 84 \times (2 \times 50 + 91) \\[1em] = 22 \times 12 \times 191 \\[1em] = 264 \times 191 \\[1em] = 50424 \text{ m}^2.

Adding 20% for folds and stitches,

Area of canvas = 50424 + 20% of 50424

$= 50424 + \dfrac{20}{100} \times 50424 \\[1em] = 50424 + 0.2 \times 50424 \\[1em] = 50424 + 10084.8 \\[1em] = 60508.8 \text{ m}^2 \\[1em] \approx 60509 \text{ m}^2$

Hence, the quantity of canvas required to make the tent is 60509 m².