Mathematics
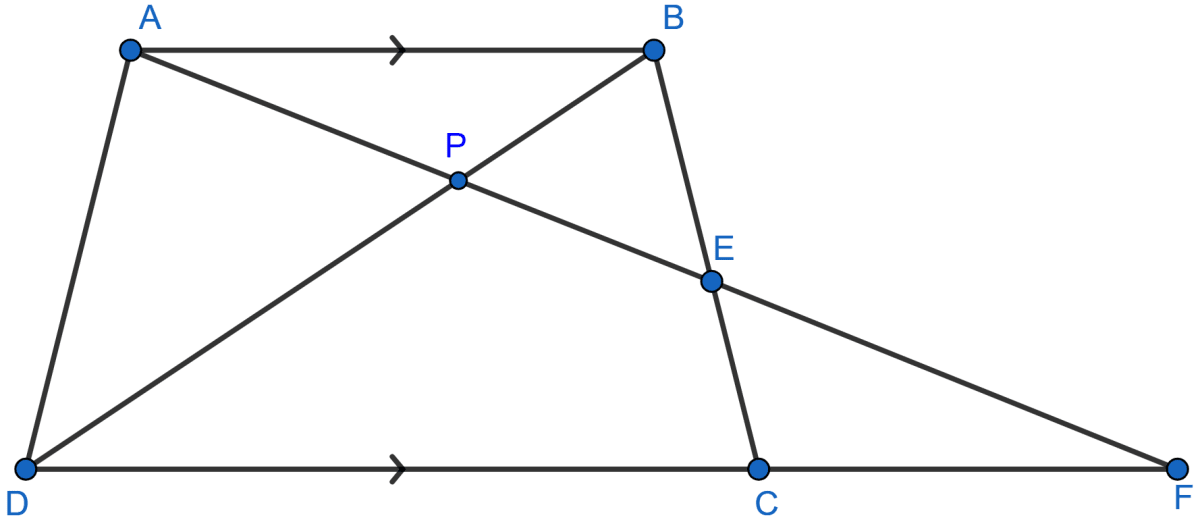
Area of triangle ADE = 9 cm2 and area of trapezium DBCE = 16 cm2.
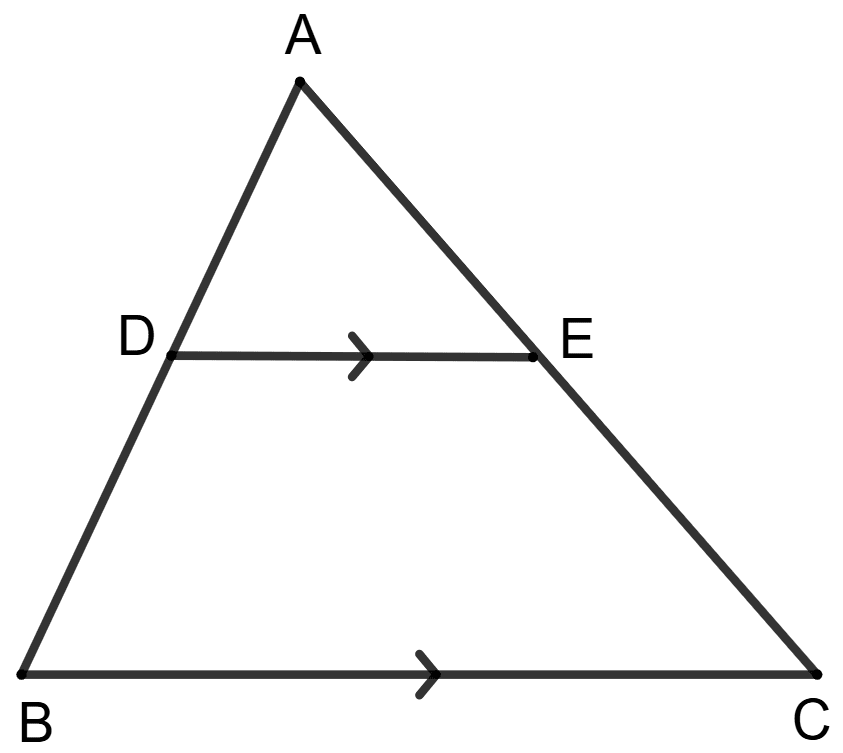
Statement (1) : .
Statement (2) : .
Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Similarity
4 Likes
Answer
Given,
Area of triangle ADE = 9 cm2 and area of trapezium DBCE = 16 cm2.
In Δ ABC and Δ ADE,
⇒ ∠BAC = ∠DAE (Common angle)
⇒ ∠ABC = ∠ADE (Corresponding angles are equal)
⇒ ∠ACB = ∠AED (Corresponding angles are equal)
∴ Δ ABC ∼ Δ ADE (By A.A.A. postulate)
From figure,
⇒ Area of triangle ABC = Area of triangle ADE + Area of trapezium DBCE = 9 + 16 = 25 cm2
We know that,
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
So, statement 1 is false but statement 2 is true.
Hence, option 4 is the correct option.
Answered By
2 Likes
Related Questions
In triangle ODQ, ∠Q = ∠BPO = 90° AB = 2 x OA, BC = 3 x OA and CD = 4 x OA.
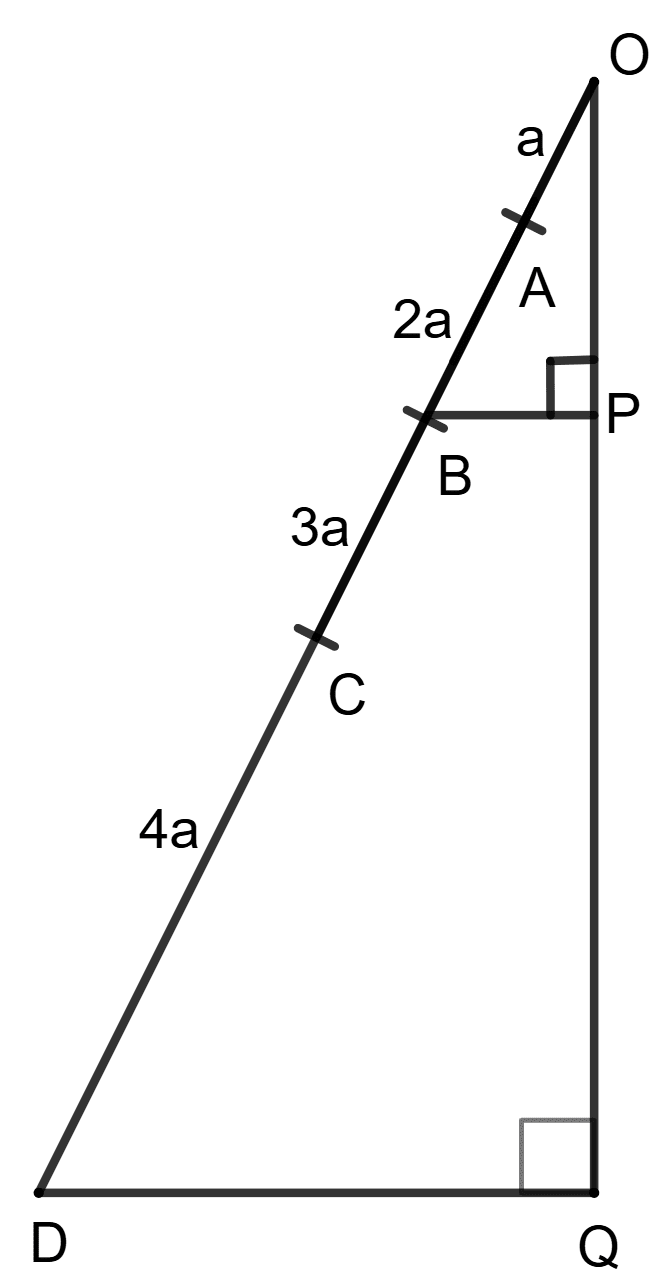
Assertion (A) : .
Reason (R) : Δ OBP - ODQ and .
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.
In triangle ABC, ∠B = 90° and in triangle ADE, ∠D = 90°.
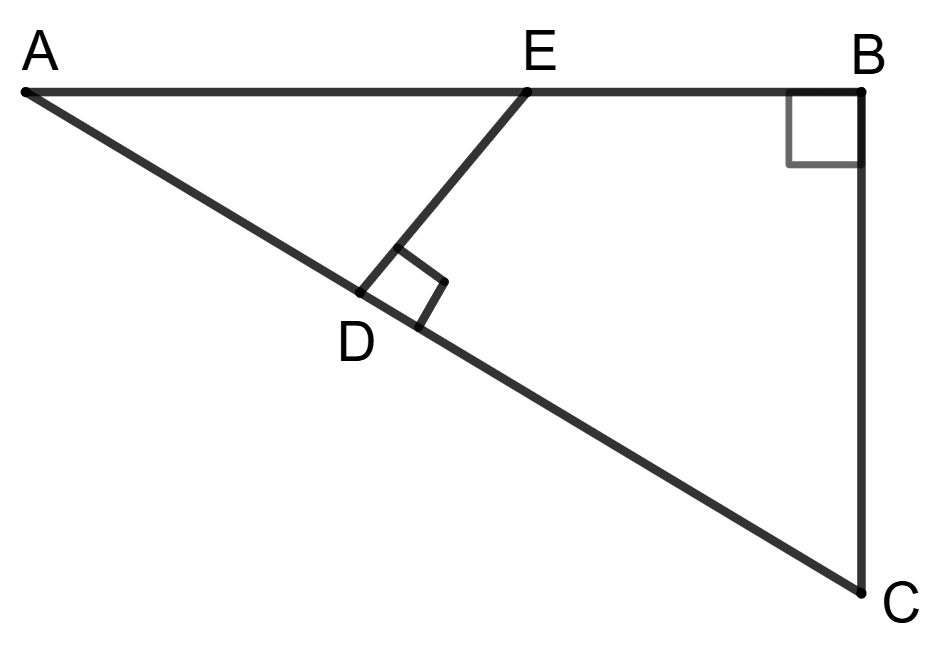
Statement (1) : .
Statement (2) : Triangle AED and ACB are similar.
Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
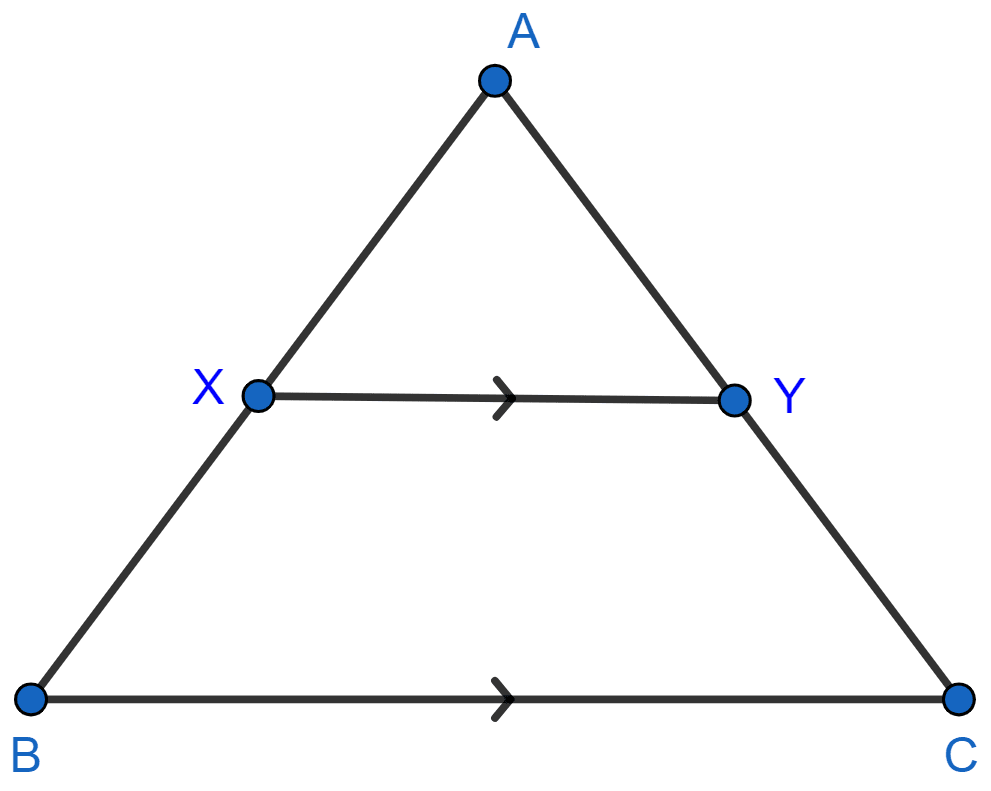
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.
Find:
(i)
(ii)
(iii) XY
In the following figure, ABCD is a trapezium with AB || DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm,
Calculate :
(i) EC (ii) AF (iii) PE