Mathematics
Arrange the sides of △ BOC in descending order of their lengths. BO and CO are bisectors of angles ABC and ACB respectively.

Triangles
13 Likes
Answer
From figure,
DAC is a straight line.
∴ ∠DAB + ∠BAC = 180°
⇒ 137° + ∠BAC = 180°
⇒ ∠BAC = 180° - 137° = 43°.
EBC is a straight line.
∴ ∠EBA + ∠ABC = 180°
⇒ 106° + ∠ABC = 180°
⇒ ∠ABC = 180° - 106° = 74°.
In △ ABC,
By angle sum property of triangle,
⇒ ∠ABC + ∠BAC + ∠ACB = 180°
⇒ 74° + 43° + ∠ACB = 180°
⇒ 117° + ∠ACB = 180°
⇒ ∠ACB = 180° - 117° = 63°.
Since, OB is the bisector of angle ABC.
∴ ∠OBC = = 37°.
Since, OC is the bisector of angle ACB.
∴ ∠OCB = = 31.5°.
In △ OBC,
By angle sum property of triangle,
⇒ ∠OBC + ∠OCB + ∠BOC = 180°
⇒ 37° + 31.5° + ∠BOC = 180°
⇒ 68.5° + ∠BOC = 180°
⇒ ∠BOC = 180° - 68.5° = 111.5°
∴ ∠BOC > ∠OBC > ∠OCB
∴ BC > CO > BO (If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.)
Hence, sides of triangle BOC in descending order are BC > CO > BO.
Answered By
9 Likes
Related Questions
If two sides of a triangle are 8 cm and 13 cm, then the length of the third side is between a cm and b cm. Find the values of a and b such that a is less than b.
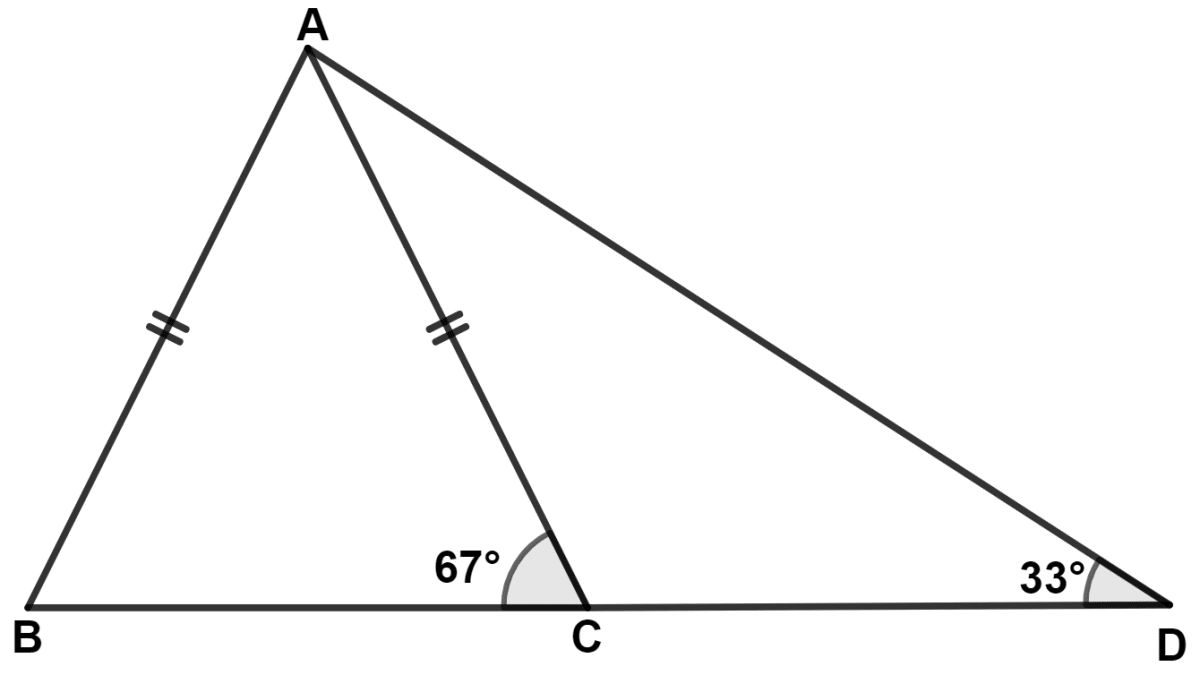
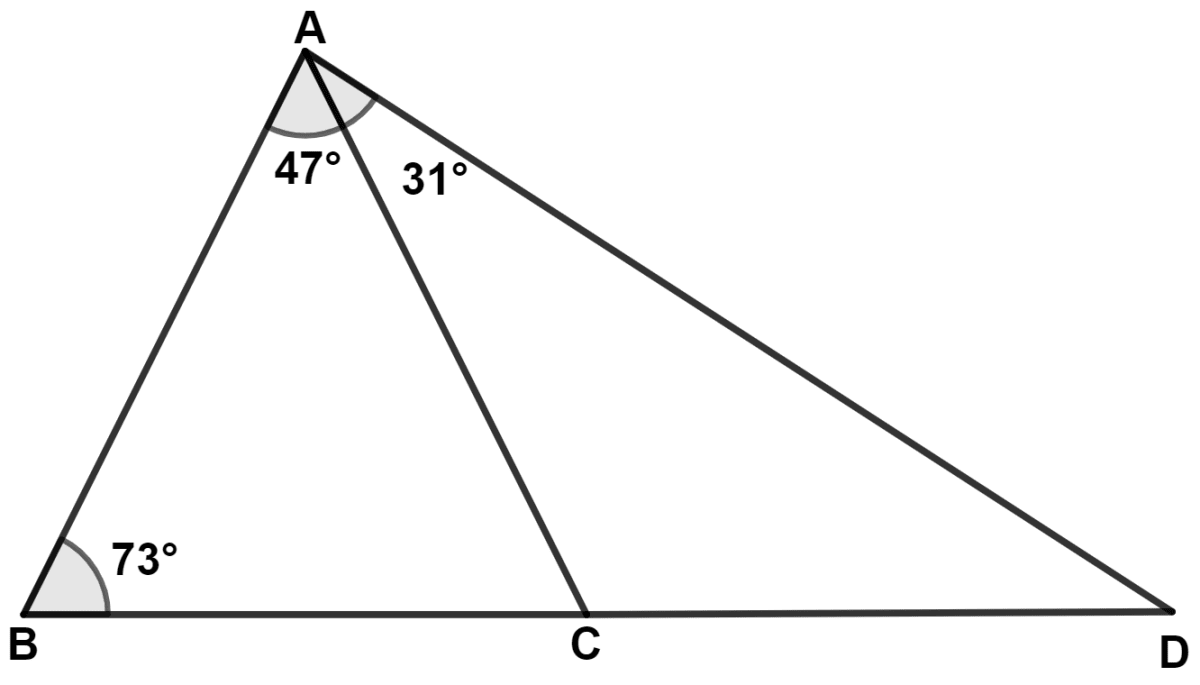
In each of the following figures, write BC, AC and CD in ascending order of their lengths.
D is a point in side BC of triangle ABC. If AD > AC, show that AB > AC.
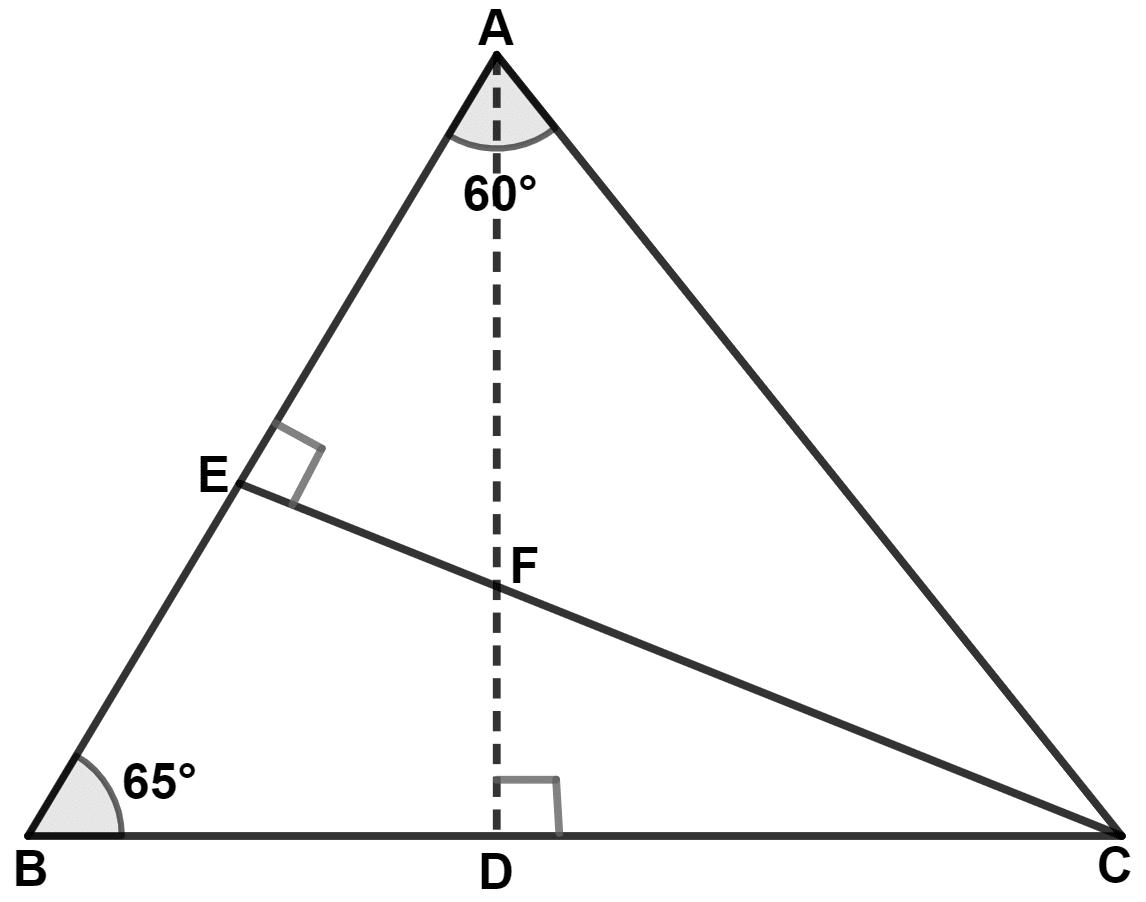
In the following figure, ∠BAC = 60° and ∠ABC = 65°. Prove that :
(i) CF > AF
(ii) DC > DF