Mathematics
Assertion (A): ABCD is a parallelogram. AX is bisector of ∠A, CY is bisector of ∠C. Then quadrilateral AXCY is also a parallelogram.
Reason (R): If any one pair of opposite sides of a quadrilateral are equal and parallel then the quadrilateral is a parallelogram.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Rectilinear Figures
1 Like
Answer
Both A and R are true.
Explanation
Given,
ABCD is a parallelogram.
The bisector of angle A intersects CD at X and bisector of angle C intersects AB at Y as shown in the figure below:
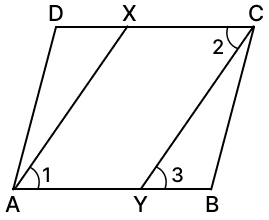
∠ A = ∠ C [∵ opposite angles in ||gm are equal]
Dividing by 2 on both sides,
=
From figure,
∠1 = ∠2 ……….[1]
Since, AB || CD with CY as transversal,
∴ ∠2 = ∠3 [∵ Alternate angles]
∴ ∠1 = ∠3 [From 1]
As corresponding angles are equal,
∴ AX || YC
In parallelogram ABCD,
AB || DC
∴ AY || XC
As, AX || YC and AY || XC,
the opposite sides of the quadrilateral AXCY are parallel
∴ AXCY is a parallelogram [∵ Opposite sides are parallel]
∴ Assertion (A) is true.
Given : ABCD is a quadrilateral such that AB = DC and AB is parallel to DC.
To Prove : ABCD is a parallelogram.
Proof : Join A and C.
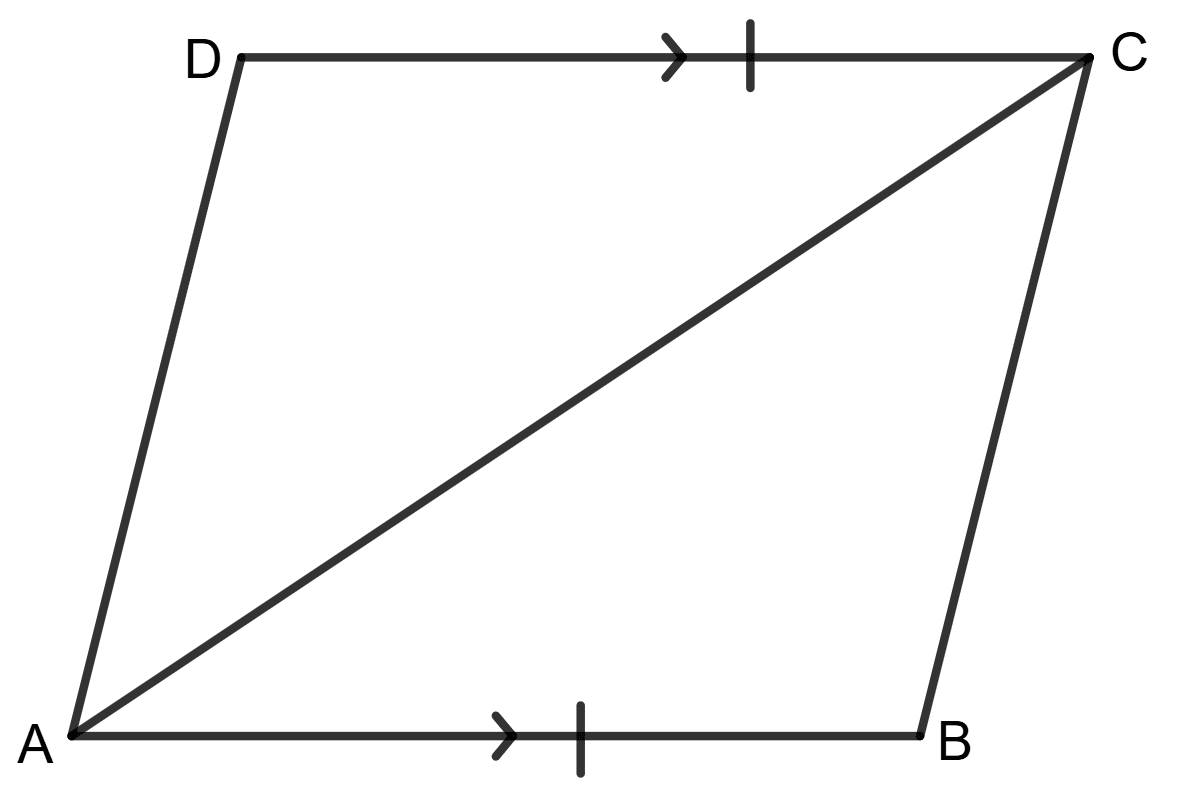
In Δ ABC and Δ CDA,
AB = CD (Given)
∠ BAC = ∠ DCA [∵ Alternate angles]
AC = AC [∵ Common side]
By SAS Congruency criterion,
Δ ABC ≅ Δ CDA
∴ ∠ BCA = ∠ DAC [∵ C.P.C.T.C.]
But, ∠ BCA and ∠ DAC are alternate angles
∴ AD || BC [∵ Alternate angles are equal]
∴ ABCD is a parallelogram [∵ Opposite sides are parallel]
∴ Reason (R) is true.
Hence, both Assertion (A) and Reason (R) are true.
Answered By
1 Like
Related Questions
Assertion (A): In a regular polygon, sum of its interior angles : sum of its external angles is 3 : 1. The number of sides (n) in it is 8.
Reason (R):
⇒
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): In the given figure, ABCD is a rectangle and DCEF is a parallelogram then ABEF is a rectangle.
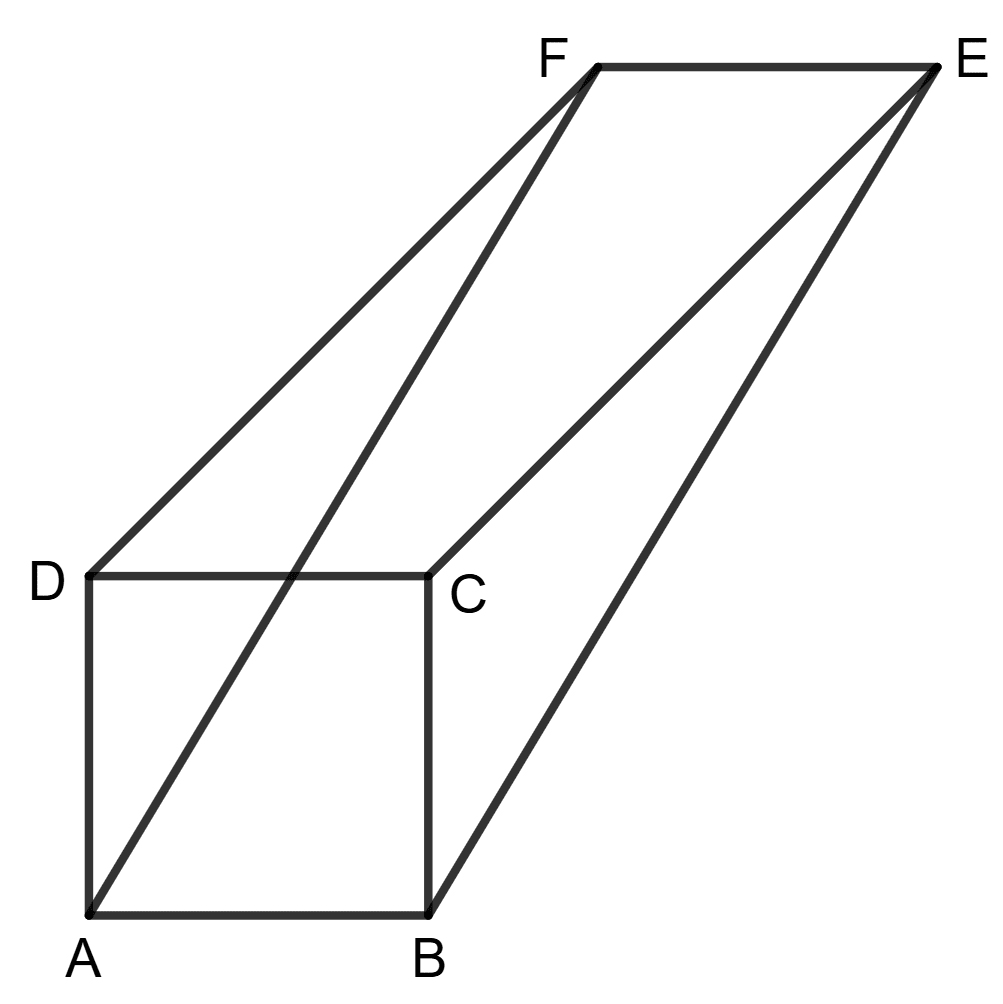
Reason (R):
AB = DC and DC = FE⇒ AB = FE and so ABEF is a rectangle.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): In the given figure, if the area of the parallelogram ABEF is 120 cm2, then area of rectangle ABCD is 120 cm2.
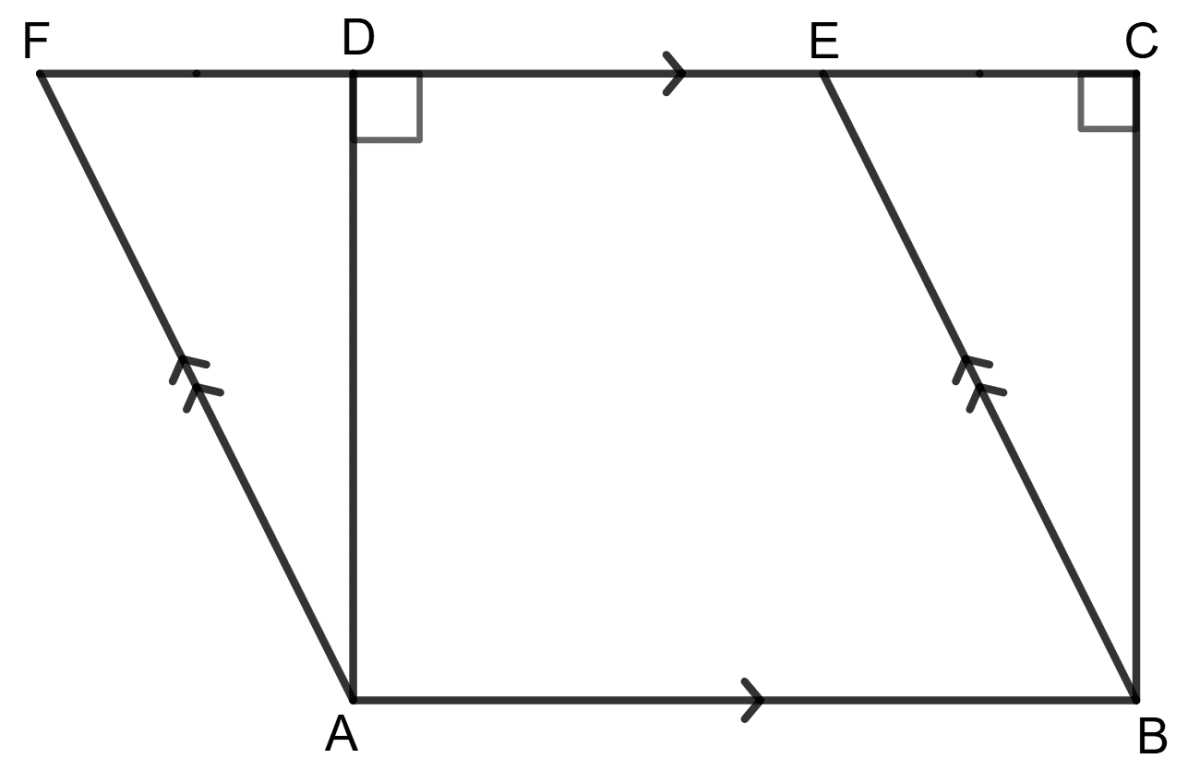
Reason (R): Parallelogram and rectangle on the same base and between the same parallels are equal in area.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): The length of the side of a regular hexagon is equal to the radius of its circumcircle.
Reason (R):
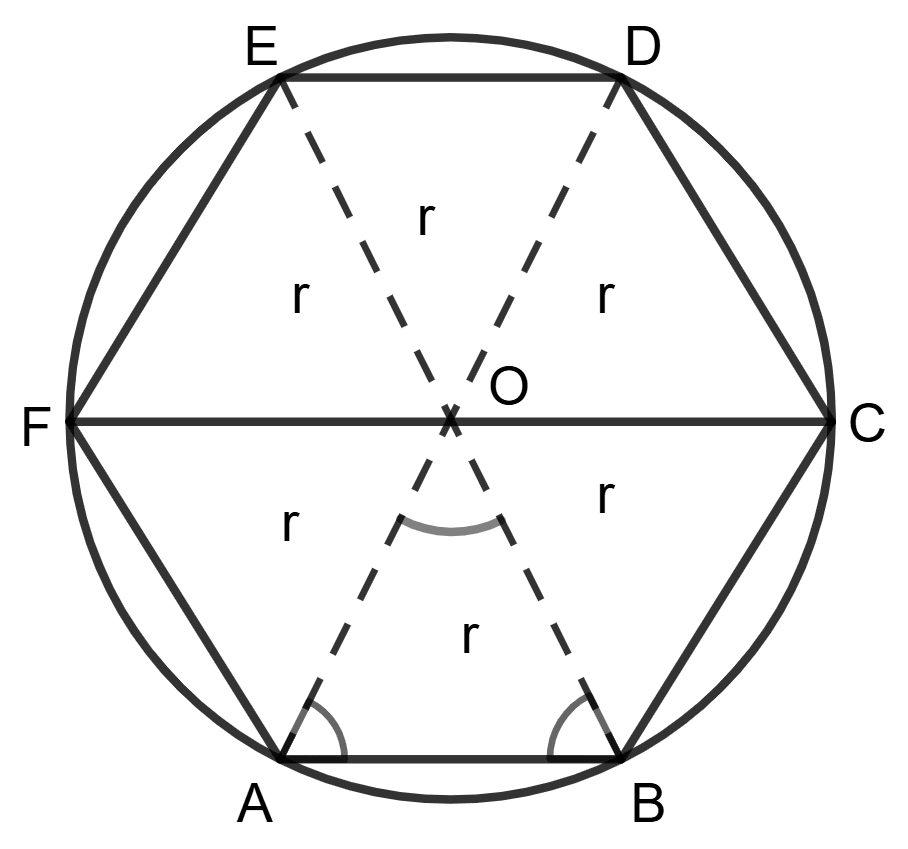
∠AOB =
∠OAB = ∠OBA =
⇒ OAB is an equilateral triangle
So, AB = OA = radius (r) of the circumcircle- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.