Mathematics
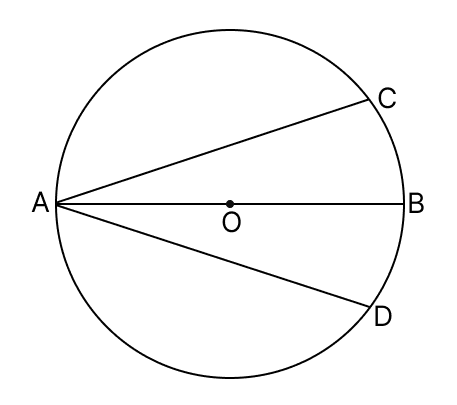
Assertion (A): In adjoining figure, AB is diameter of the circle with centre O.
If chord AC = chord AD, then we can conclude that ars BC = arc DB.
Reason (R): In adjoining figure, we can conclude that if chord AC = chord AD, then arc AC = arc AD.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
Given,
AB is the diameter of the circle with center O and, Chord AC = Chord AD.
We know that in a circle, equal chords subtend equal arcs.
⇒ arc AC = arc AD = x (let) ……………………(1)
∴ Reason (R) is true.
AB is a diameter of the circle.
As we know that the diameter of a circle divides the circle into two equal arcs.
⇒ arc ACB = arc ADB.
⇒ arc AC + arc BC = arc AD + arc DB.
From equation (1), we get :
⇒ x + arc BC = x + arc DB.
⇒ arc BC = arc DB.
∴ Assertion (A) is true.
∴ Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Hence, option 3 is the correct option.
Related Questions
Assertion (A): Equal chords of a circle are equidistant from centre.
Reason (R): Chords of a circle that are equidistant from the centre of a circle are equal.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Assertion (A): In a circle, equal arcs suspend equal angles at the centre.
Reason (R): In the same circle, equal chords cuts off equal arc.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
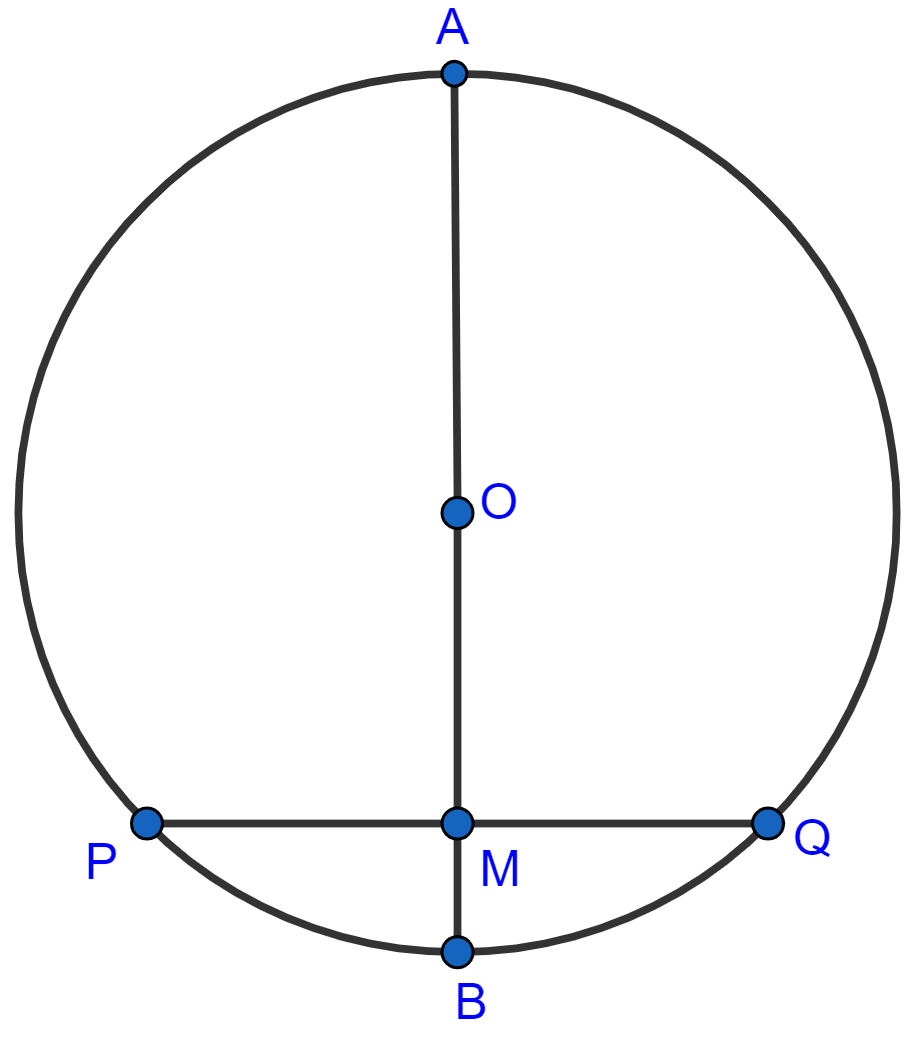
In the adjoining figure, a chord PQ of a circle with center O and radius 15 cm is bisected at M by a diameter AB. If OM = 9 cm, find the lengths of :
(i) PQ
(ii) AP
(iii) BP.
The radii of two concentric circles are 17 cm and 10 cm; a line PQRS cuts the larger circle at P and S and the smaller circle at Q and R. If QR = 12 cm, calculate PQ.