Mathematics
Assertion (A): Area of given rhombus = 10 cm x 10 cm = 100 cm2
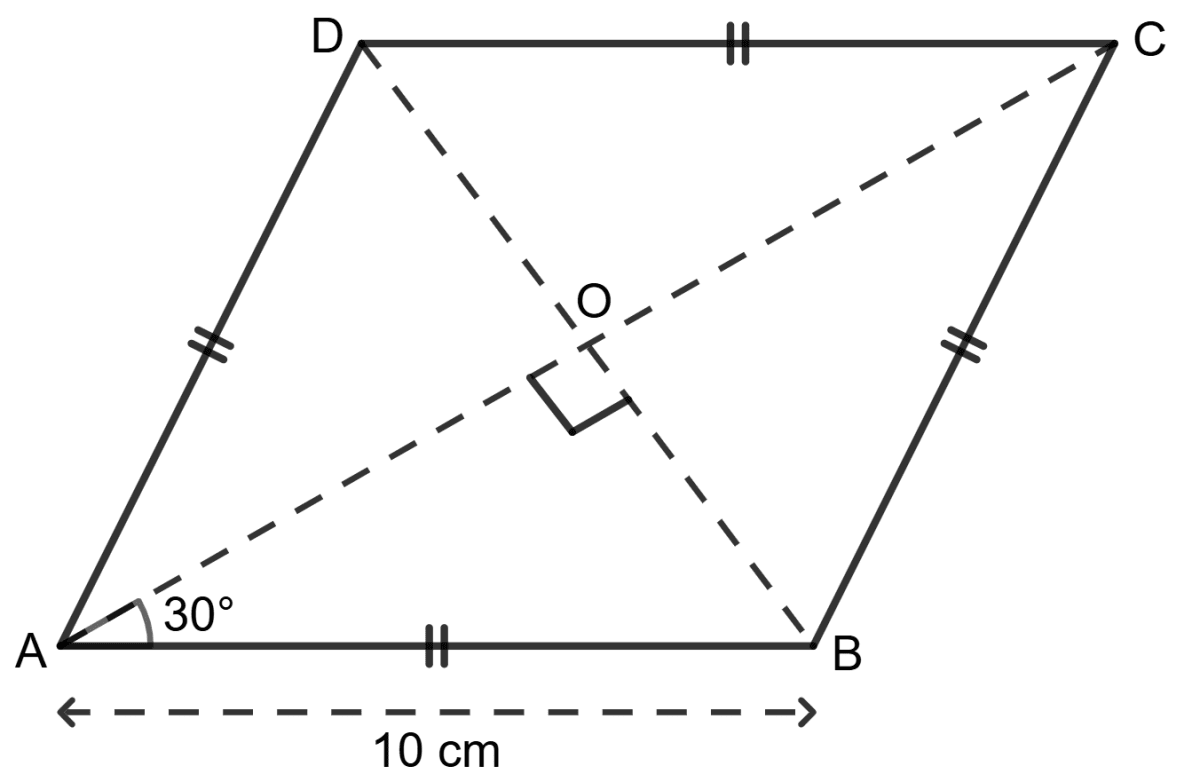
Reason (R):
⇒ OA = cm
⇒ AC = 2 x cm = cm
⇒ OB = 5 cm
⇒ BD = 2 x 5 cm = 10 cm
Area of rhombus ABCD = AC x BD = 10 x 10 cm2 = 100 cm2
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Trigonometric Identities
3 Likes
Answer
Both A and R are false.
Explanation
We know that the diagonal of a rhombus bisect each other at right angles and also bisect the angle of the vertex.
⇒ OA = OC = AC
⇒ OB = OD = BD
∠ AOB = 90°
∠ OAB = 30°
In Δ AOB,
sin 30° =
⇒
⇒ OB
⇒ OB = 5 cm
And, cos 30° =
⇒
⇒ OA
⇒ OB = 5 cm = 8.66 cm
So, AC = 2 x OA = 2 x 8.66 cm
= 17.32 cm
And, BD = 2 x OB = 2 x 5 cm
= 10 cm
Area of rhombus = x product of diagonals
= x 17.32 x 10 cm2
= 17.32 x 5 cm2
= 86.6 cm2
According to Assertion, Area of rhombus = 10 cm x 10 cm = 100 cm2 (≠ 86.6 cm2).
∴ Assertion (A) is false.
Given, OA = cm
⇒ AC = 2 x cm = cm
And, OB = 5 cm
⇒ BD = 2 x 5 cm = 10 cm
Area of rhombus ABCD = AC x BD = x 10 cm2 = 100 cm2
∴ Reason (R) is false.
Hence, both Assertion (A) and Reason (R) are false.
Answered By
1 Like
Related Questions
Assertion (A): If ∠A = 30°, the value of tan2 2A - sec2 2A is 1.
Reason (R): tan2 2A - sec2 2A = tan2 60° - sec2 60°
=- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): If 2 cos 3A = 1, A = 20°.
Reason (R): cos 3A = ⇒ 3A = 60° ⇒ A = 20°
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): CD = 3 x AB = 3 x 10 m = 30 m
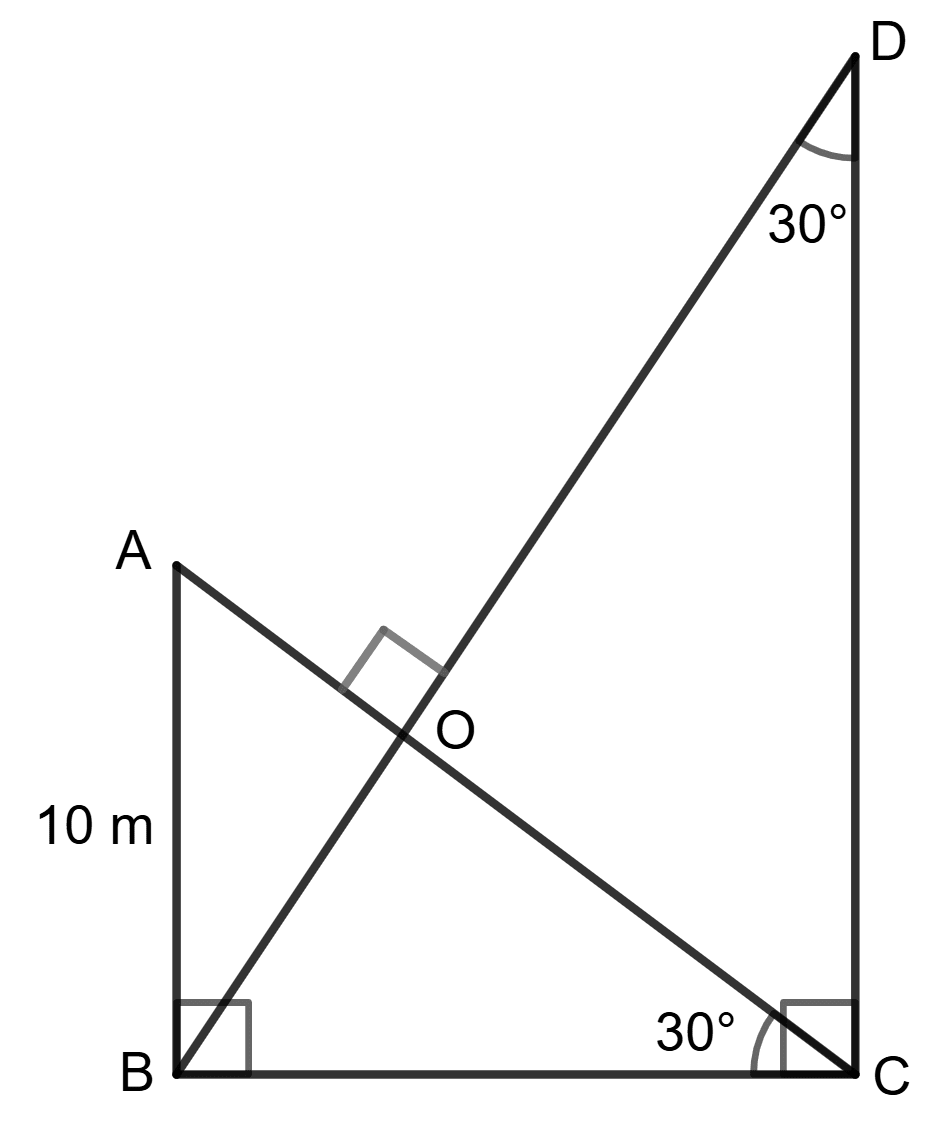
Reason (R): In △ABC, tan30° =
⇒ BC = 10 m
tan 30° =
⇒ CD = 30 m- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): If cosec (90° - 3A) = 1; angle A is 30°.
Reason (R):
cosec (90° - 3A) = 1
⇒ 90° - 3A = 90°
⇒ A = 0°- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.