Mathematics
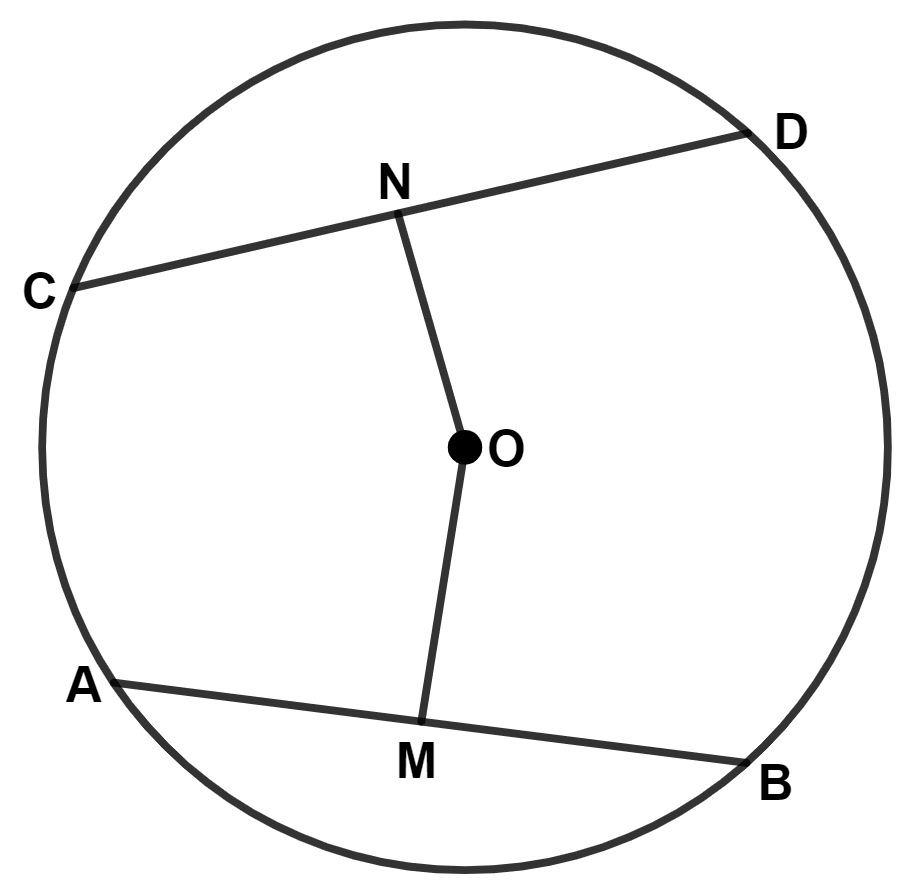
Assertion (A): In the given figure, chord AB = 8 cm, diameter CD = 20 cm, then length of OP = 10 cm.
Reason (R): OP =
and CP = OC + OP
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Circles
2 Likes
Answer
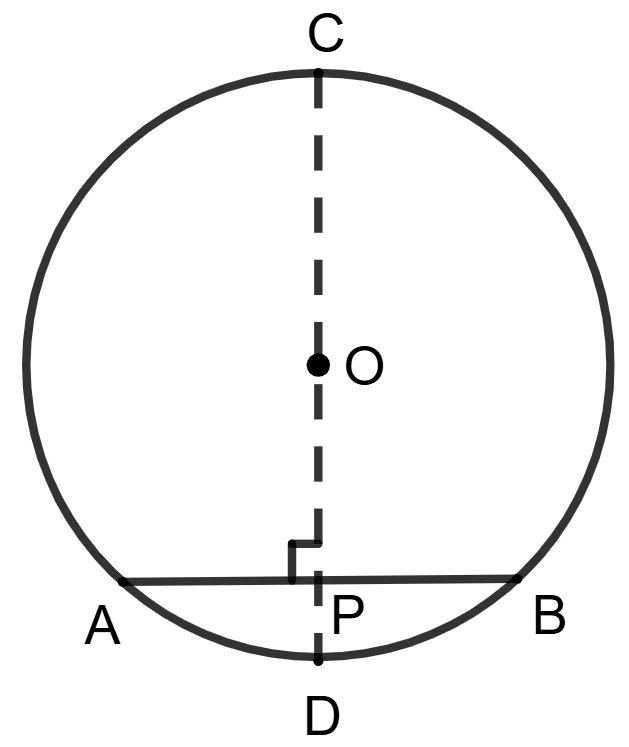
Given:
Length of the chord AB = 8 cm.
Diameter of the circle CD = 20 cm.
As we know that the radius of a circle is exactly half its diameter.
Radius of the circle, r = = 10 cm.
Construction: Join OA.
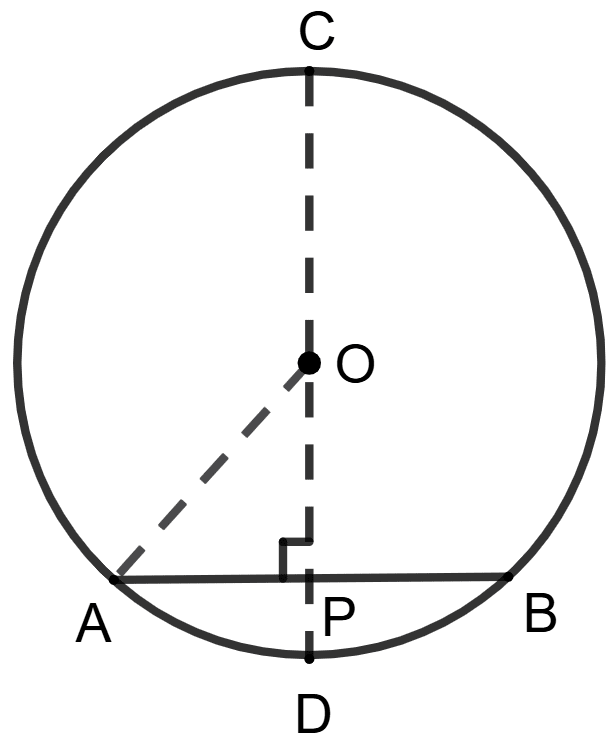
OP ⊥ AB.
Since, perpendicular drawn from the center of a circle to a chord bisects it.
∴ OP bisects AB
⇒ AP = x AB = x 8 = 4 cm
⇒ OA = 10 cm
In Δ OAP, ∠P = 90°
Using Pythagoras theorem,
∴ OA2 = OP2 + AP2
⇒ OP2 = OA2 - AP2
∴ Assertion (A) is false.
From figure, CP = CO + OP = 10 + 2 cm
∴ Reason (R) is true.
∴ A is false, but R is true.
Hence, option 2 is the correct option.
Answered By
1 Like
Related Questions
Statement 1: O and O' are centres of two equal circles and ABCD is a straight line.
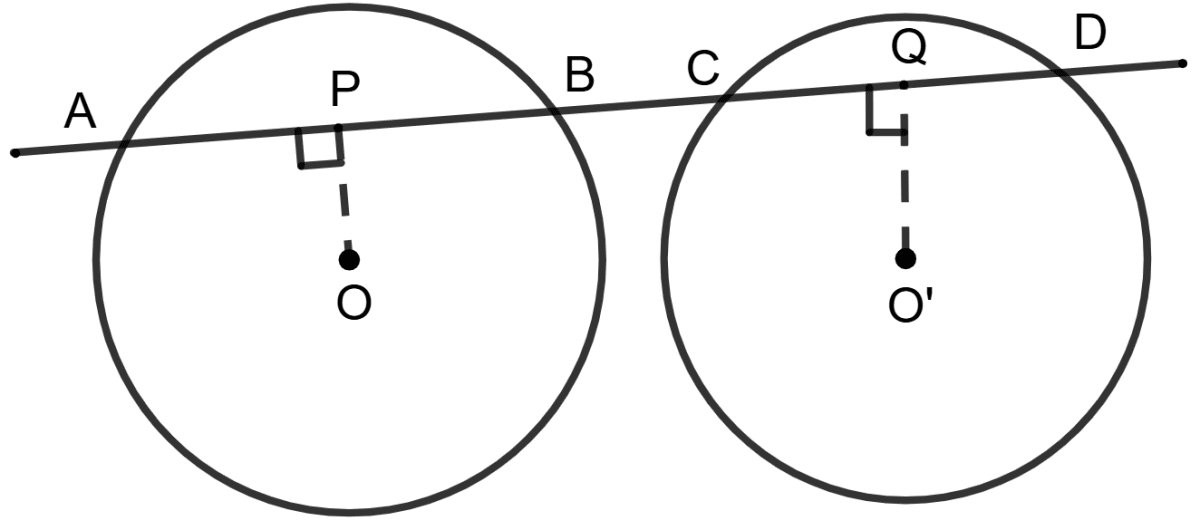
Statement 2: If OP ⊥ AB, O'Q ⊥ CD and O'Q is greater than OP, then CD > AB.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Statement 1: In a circle with center O, chord AB : chord BC = 1 : 3. If angle AOC is 160° ⇒ angle BOC = 120°.
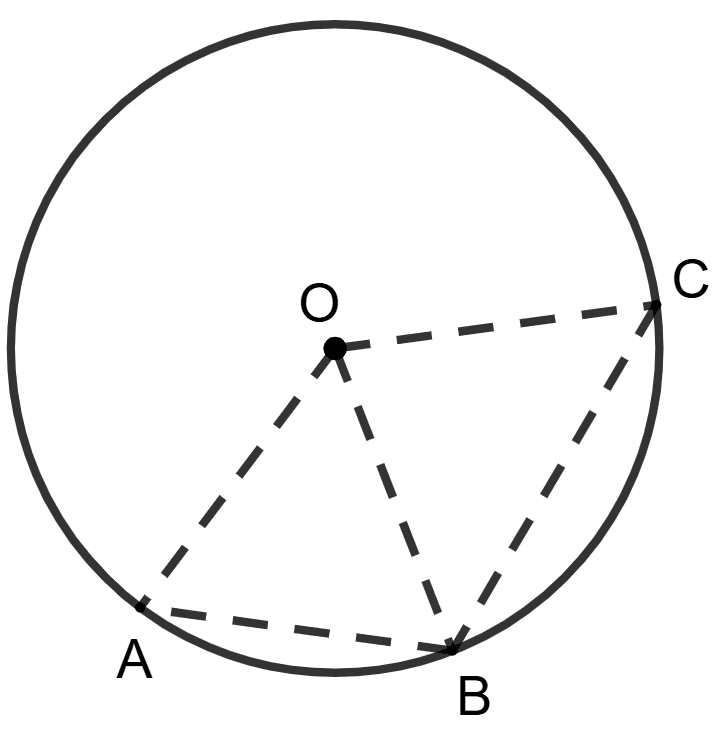
Statement 2: AB : BC = 1 : 3
⇒ ∠AOC = 3 x ∠AOB
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
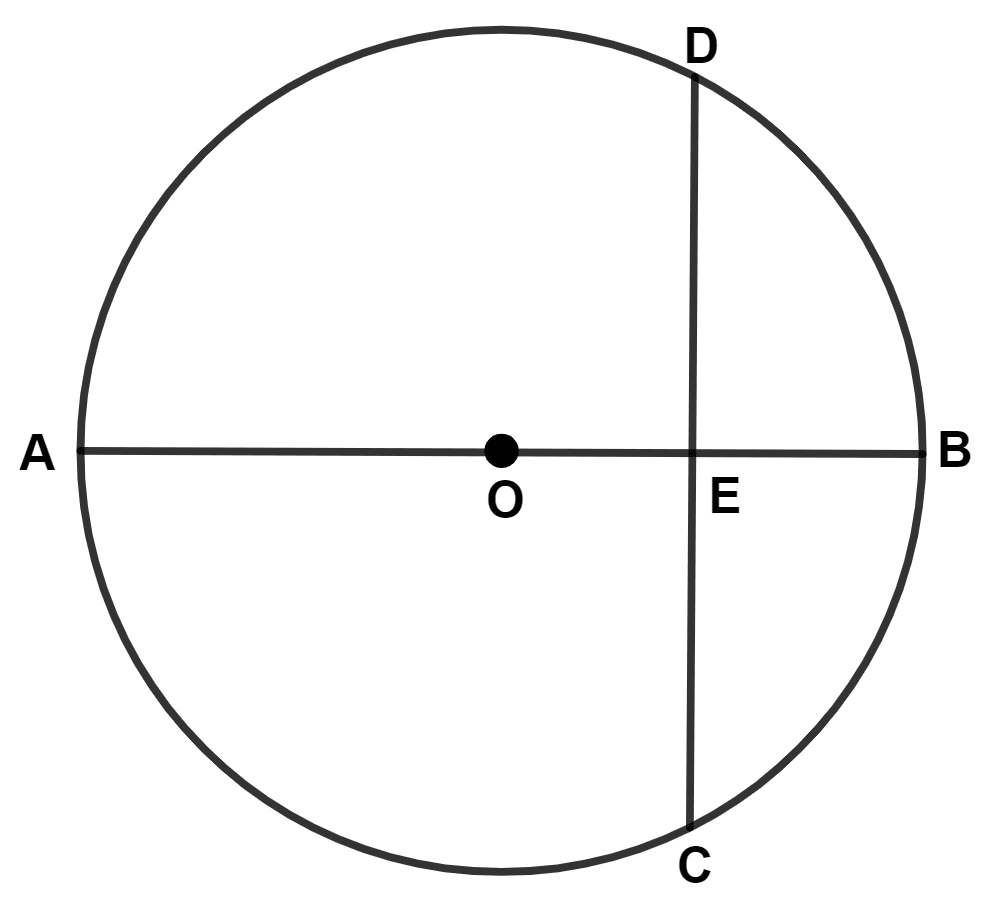
The figure, given below, shows a circle with center O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm, find the radius of the circle.
In the given figure, O is the center of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the :
(i) the radius of the circle
(ii) length of chord CD.