KnowledgeBoat Logo
|

Mathematics

Assertion (A) : In a parallelogram, the bisectors of any two pair of adjacent angles meet at right angle.

Reason (R) : In a parallelogram opposite angles are equal.

  1. Both A and R are correct, and R is the correct explanation for A.

  2. Both A and R are correct, and R is not the correct explanation for A.

  3. Statement 1 is true, and statement 2 is false.

  4. Statement 1 is false, and statement 2 is true.

Quadrilaterals

3 Likes

Answer

Let ABCD be the parallelogram. AO and BO be the bisector of angles A and B respectively.

∴ ∠BAO = ∠A2\dfrac{∠A}{2} and ∠ABO = ∠B2\dfrac{∠B}{2}

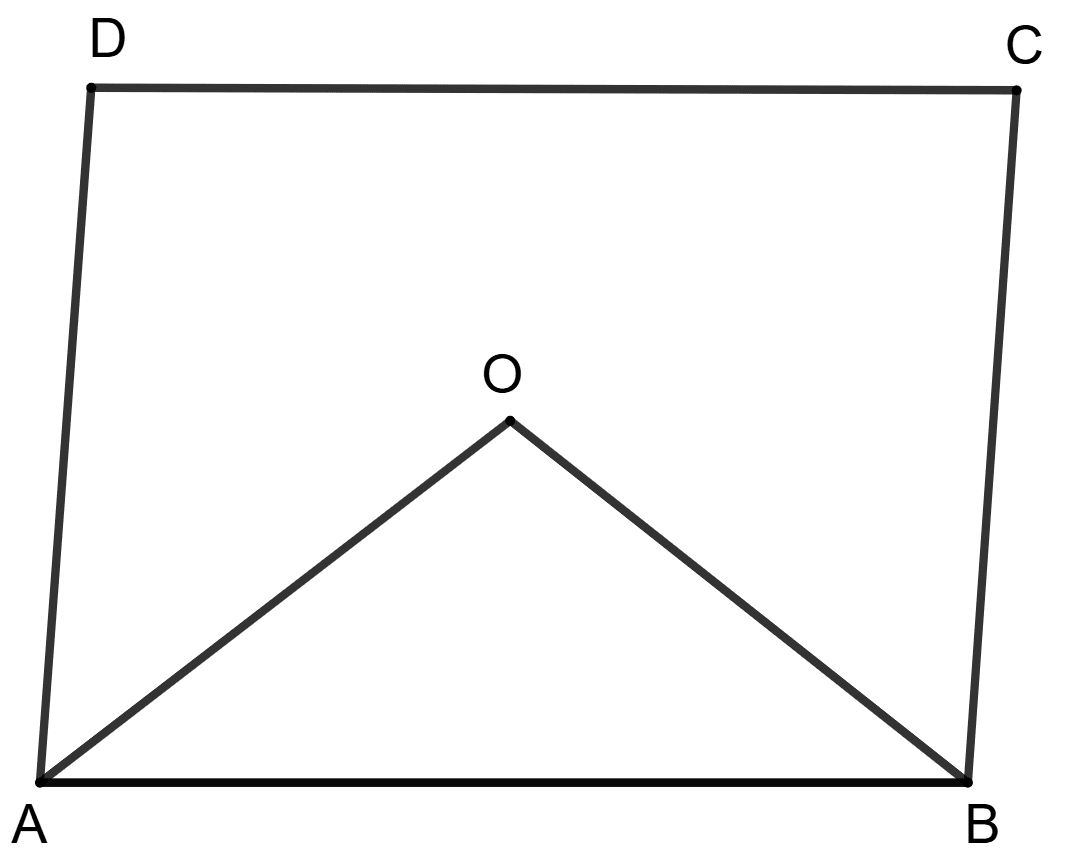
Let ABCD be the parallelogram. AO and BO be the bisector of angles A and B respectively. ∠BAO = ∠A/2 and ∠ABO = ∠B/2. Special Types Of Quadrilaterals, Concise Mathematics Solutions ICSE Class 8.

We know that in a parallelogram, consecutive angles are supplementary.

⇒ ∠A + ∠B = 180°

⇒ 12\dfrac{1}{2} (∠A + ∠B) = 12\dfrac{1}{2} x 180°

⇒ 12∠A+12∠B\dfrac{1}{2} ∠A + \dfrac{1}{2} ∠B = 90°

In ΔAOB, according to angle sum property

⇒ ∠AOB + ∠ABO + ∠BAO = 180°

⇒ ∠AOB + 12∠B+12∠A\dfrac{1}{2}∠B + \dfrac{1}{2}∠A = 180°

⇒ ∠AOB + 90° = 180°

⇒ ∠AOB = 180° - 90°

⇒ ∠AOB = 90°

Thus, the bisector of any two pair of adjacent angles meet at right angle.

So, assertion (A) is true.

We know that,

The opposite angles of a parallelogram are equal.

∴ Reason (R) is true.

∴ Both A and R are correct, and R is not the correct explanation for A.

Hence, option 2 is the correct option.

Answered By

2 Likes

Related Questions