Mathematics
Assertion (A): In a regular polygon, sum of its interior angles : sum of its external angles is 3 : 1. The number of sides (n) in it is 8.
Reason (R):
⇒
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Rectilinear Figures
2 Likes
Answer
Both A and R are true.
Explanation
Let the regular polygon has n number of sides.
Sum of interior angles of an n sided polygon = Sinterior = (2n - 4) x 90°
Sum of exterior angles of an n sided polygon = Sexterior = 360°
∴ Assertion (A) is true.
From assertion, n = 8.
∴ Reason (R) is true.
Hence, both Assertion (A) and Reason (R) are true.
Answered By
3 Likes
Related Questions
Assertion (A): From the information given in the figure, AP = 10 cm.
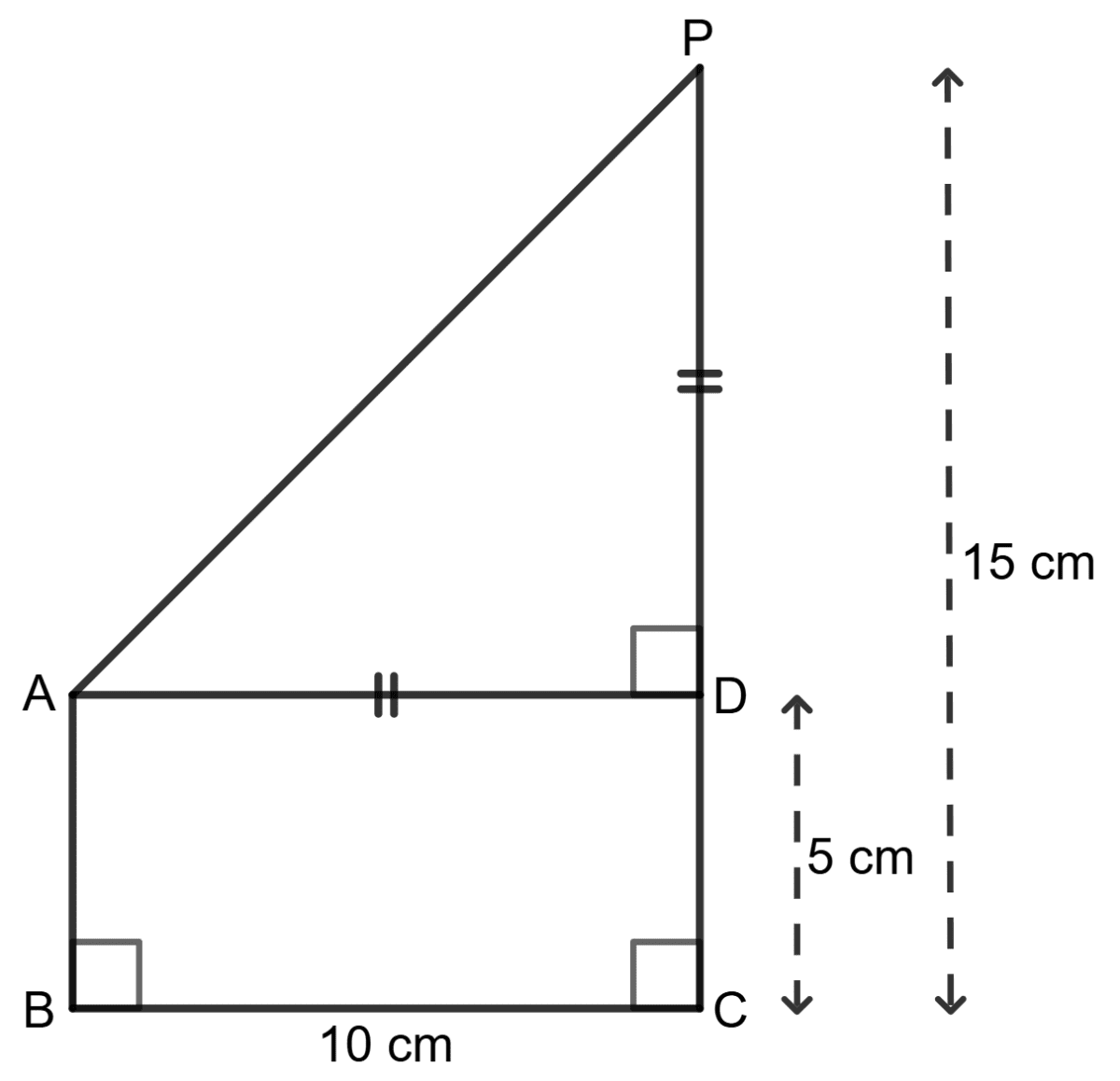
Reason (R):
⇒ AP2 = AD2 + DP2
⇒ AP2 = 102 + 102
AP =- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): According to the information in the given figure, the length of BC = 10 cm.

Reason (R):
∴ AB = AC - BC = 11 cm- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): In the given figure, ABCD is a rectangle and DCEF is a parallelogram then ABEF is a rectangle.
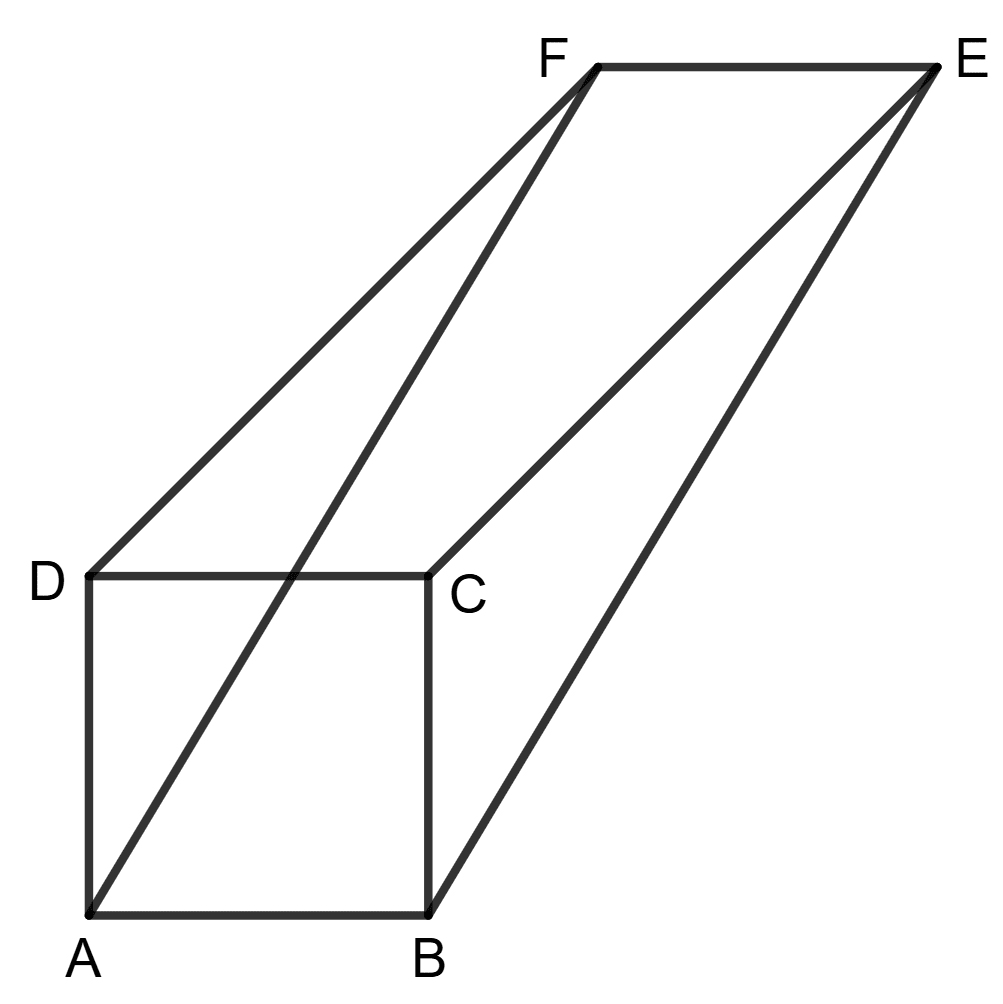
Reason (R):
AB = DC and DC = FE⇒ AB = FE and so ABEF is a rectangle.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): ABCD is a parallelogram. AX is bisector of ∠A, CY is bisector of ∠C. Then quadrilateral AXCY is also a parallelogram.
Reason (R): If any one pair of opposite sides of a quadrilateral are equal and parallel then the quadrilateral is a parallelogram.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.