Assertion (A): If sin2 A + sin A = 1 then cos4 A + cos2 A = 1. Statement 2: 1 - sin2 A = cos2 A 1. (A) is true, (R) is false. 2. (A) is false, (R) is true. 3. Both (A) and (R) are true, and (R) is the correct reason for (A). 4. Both (A) and (R) are true, and (R) is the incorrect reason for (A).

Question

KnowledgeBoat · Accepted Answer

Given, ⇒ sin2 A + sin A = 1 ⇒ sin A = 1 - sin2 A ⇒ sin A = cos2 A Squaring both the sides, we get : ⇒ (sin A)2 = (cos2 A)2 ⇒ sin2 A = cos4 A ......................(1) Solving L.H.S. of cos4 A + cos2 A = 1, we get : ⇒ cos4 A + cos2 A ⇒ sin2 A + cos2 A [From equation (1)] ⇒ 1. Since, L.H.S. = R.H.S. ∴ Assertion (A) is true. As we know that, sin2 A + cos2 A = 1 ⇒ 1 - sin2 A = cos2 A ∴ Reason (R) is true. ∴ Both (A) and (R) are true, and (R) is the correct reason for (A). Hence, option 3 is the correct option.

Mathematics

Assertion (A): If sin² A + sin A = 1 then cos⁴ A + cos² A = 1.
Statement 2: 1 - sin² A = cos² A
(A) is true, (R) is false.
(A) is false, (R) is true.
Both (A) and (R) are true, and (R) is the correct reason for (A).
Both (A) and (R) are true, and (R) is the incorrect reason for (A).

Trigonometric Identities

Answer

Related Questions

A man invested in a company paying 12% dividend on its share. If the percentage return on his investment is 10%, then the shares are:
at par
below par
above par
cannot be determined

In the given diagram ΔABC ∼ ΔEFG. If ∠ABC = ∠EFG = 60°, then the length of the side FG is:
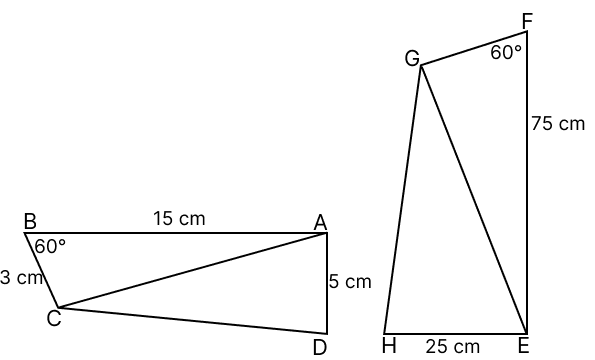
15 cm
20 cm
25 cm
30 cm

If the volume of two spheres is in the ratio 27: 64, then the ratio of their radii is:
3 : 4
4 : 3
9 : 16
16 : 9

Mathematics

Assertion (A): If sin2 A + sin A = 1 then cos4 A + cos2 A = 1.Statement 2: 1 - sin2 A = cos2 A(A) is true, (R) is false.(A) is false, (R) is true.Both (A) and (R) are true, and (R) is the correct reason for (A).Both (A) and (R) are true, and (R) is the incorrect reason for (A).