Mathematics
Assertion (A): Two triangles having equal area are congruent.
Reason (R): Two congruent triangles have equal area.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Theorems on Area
3 Likes
Answer
Having equal areas does not necessarily mean two triangles are congruent.Congruent triangles must have the same shape and the same size.
Triangles with the same area can have different shapes.
∴ Assertion (A) is false.
Congruent triangles are identical in every aspect; they have the same shape and the same size.
If two figures are identical in size, they must occupy the same amount of space, and therefore, they must have the same area.
∴ Reason (R) is true.
∴ Assertion (A) is false, Reason (R) is true.
Hence, option 2 is the correct option.
Answered By
1 Like
Related Questions
Assertion (A): Area of trapezium = (sum of parallel sides) x height.
Reason (R): A parallelogram and a rectangle on the same base and between the same parallel lines are equal in area.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
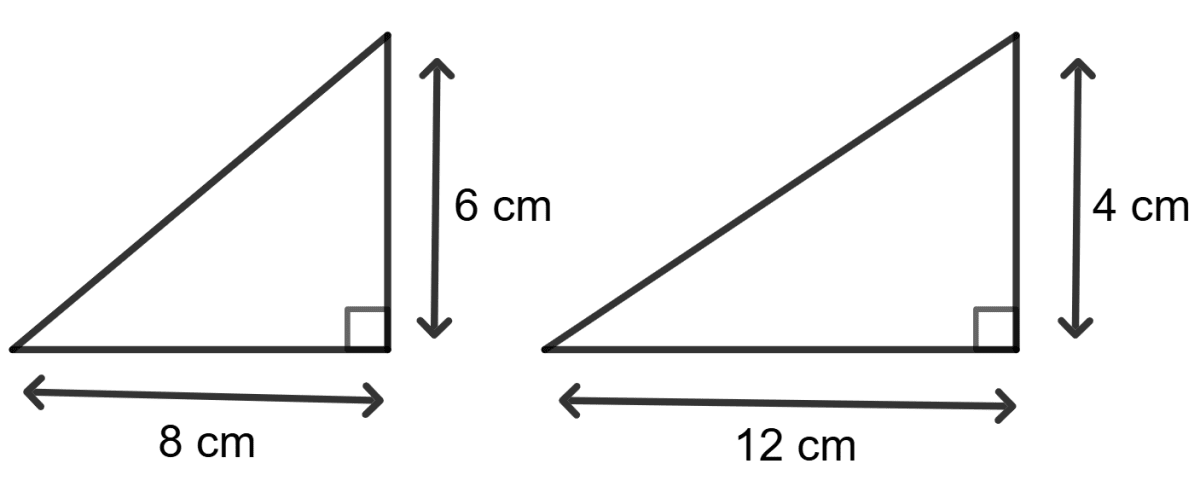
Assertion (A): In the adjoining figure, the two triangles are equal figures.
Reason (R): Two figures are called equal if and only if they have the same area.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
In the figure (1) given below, ABCD is a rectangle (not drawn to scale) with side AB = 4 cm and AD = 6 cm. Find
(i) the area of parallelogram DEFC
(ii) area of △EFG.

In the figure (2) given below, PQRS is a parallelogram formed by drawing lines parallel to the diagonals of a quadrilateral ABCD through its corners. Prove that area of || gm PQRS = 2 × area of quad. ABCD.