Mathematics
Assertion (A): Using the information in the given figure, we get : ∠PQR = ∠PSR = 90°
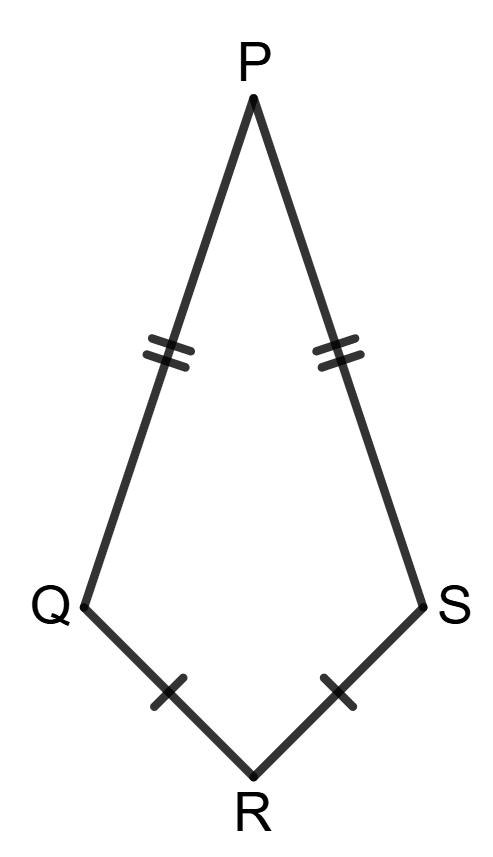
Reason (R):
By SSS, △PQR = △PSR
⇒ ∠PQR = ∠PSR
Since, ∠PQR + ∠PSR ≠ 180°
∴ ∠PQR = ∠PSR ≠ 90°
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Triangles
1 Like
Answer
A is false, R is true.
Explanation
Given,
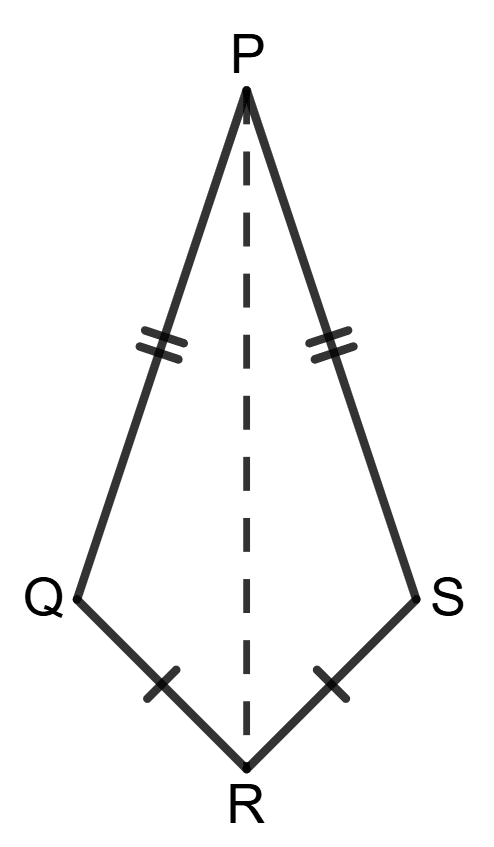
Join PR.
In △PQR and △PSR,
PR (Common side)
PQ = PS (Given)
QR = RS (Given)
∴ △PQR ≅ △PSR (By SSS)
By C.P.C.T.C.
∠PQR = ∠PSR
∠RPQ = ∠RPS
∠PRQ = ∠PRS
Assuming, ∠PQR = ∠PSR = 90°
⇒ ∠QPS = QRS = 90° [∵ Sum of interior ∠s of quadrilateral is 360°]
So, PQRS should be a rectangle with all it's angles equal to 90°.
But PQRS is not a rectangle as opposite sides are not equal.
PS ≠ QR and PQ ≠ SR
Hence our assumption ∠PQR = ∠PSR = 90° is incorrect.
∴ ∠PQR = ∠PSR ≠ 90°
∴ Assertion (A) is false.
∴ Reason (R) is true.
Hence, Assertion (A) is false, Reason (R) is true.
Answered By
1 Like
Related Questions
Assertion (A): In the given figure, the diagonals of quadrilateral bisect each other at right angle. Then △AOB ≅ △COB.
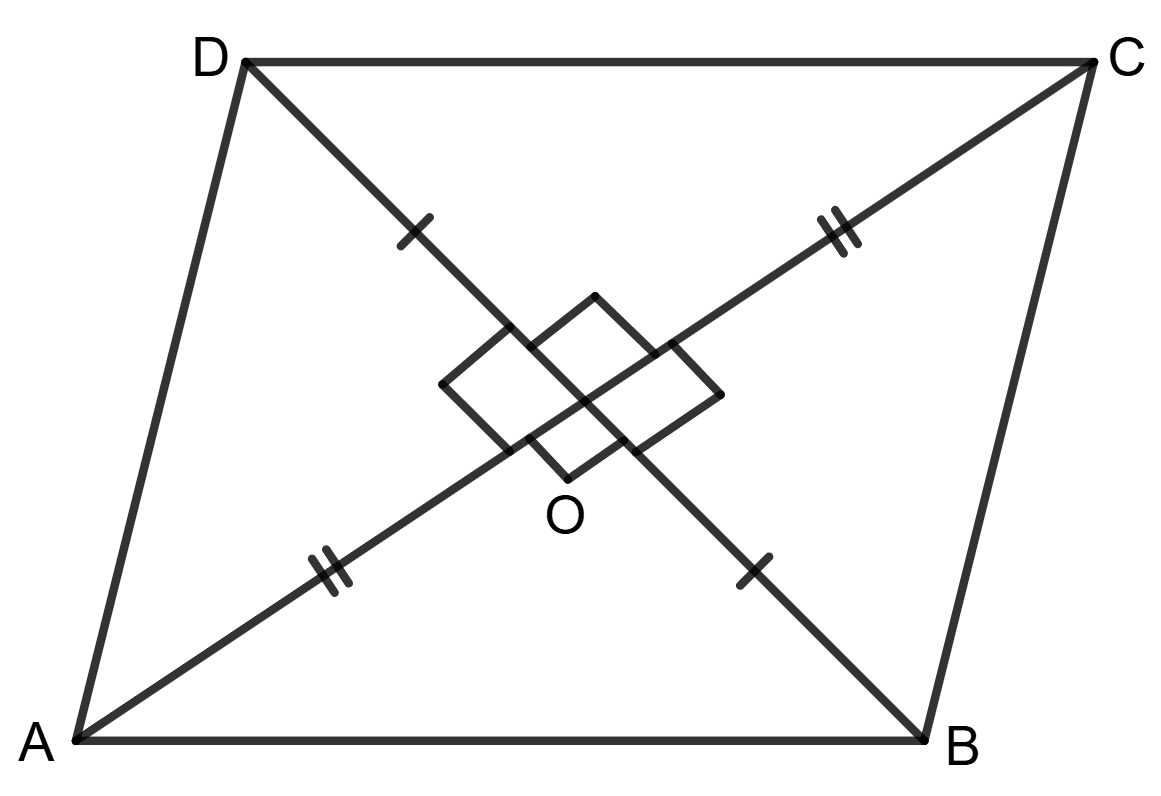
Reason (R): Two right-angled triangles are congruent, if the hypotenuse and one side of one triangle are equal to the hypotenuse and corresponding side of the other triangle.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): Using the information in the given figure, we get x = 40°.
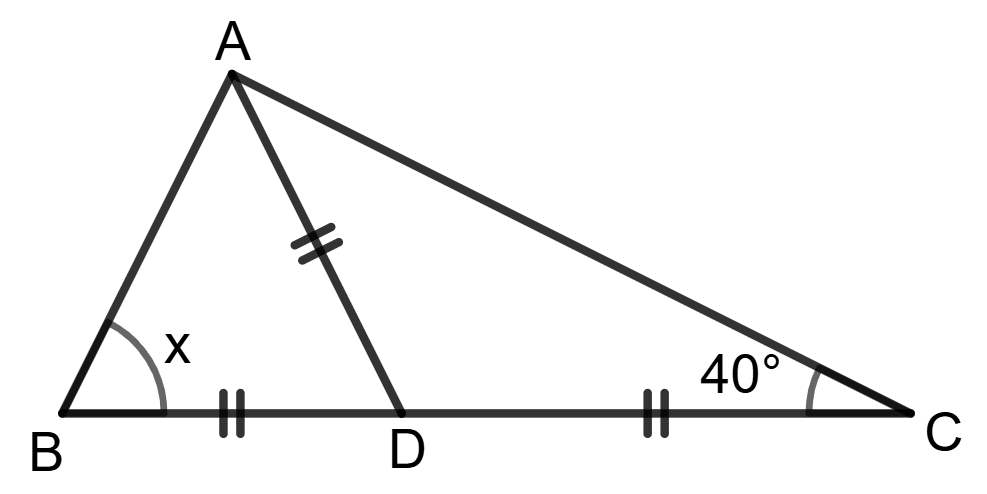
Reason (R):
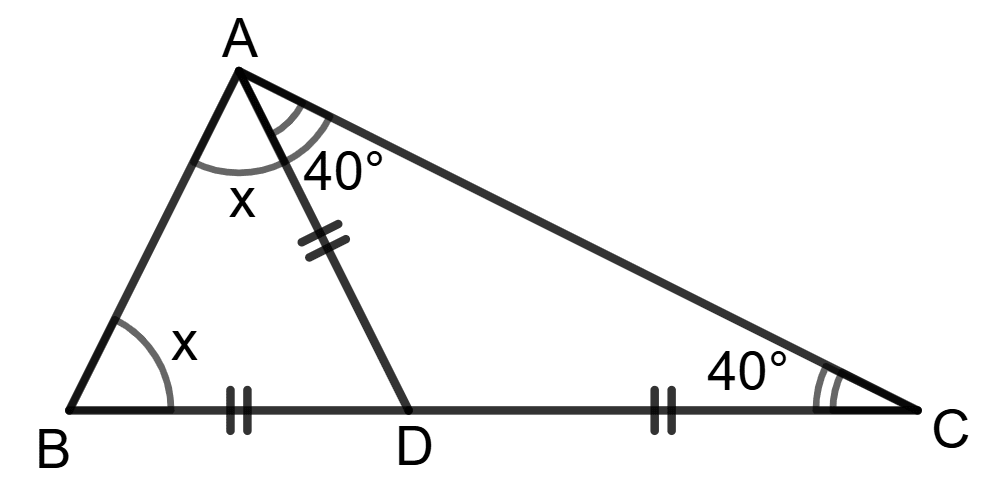
⇒ x + (x + 40°) + 40° = 180°
x = 50°- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): A, B and C are three points. If AB = 8 cm, BC = 12 cm and AC = 25 cm. Points A, B and C do not form triangle ABC.
Reason (R):
AB + BC = 8cm + 12 cm = 20 cm
and AC = 25 cm
∴ AB + BC ≯ ACPoints A, B and C do not form triangle ABC.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): Using the information in the given figure, we get BC > AB > AC.
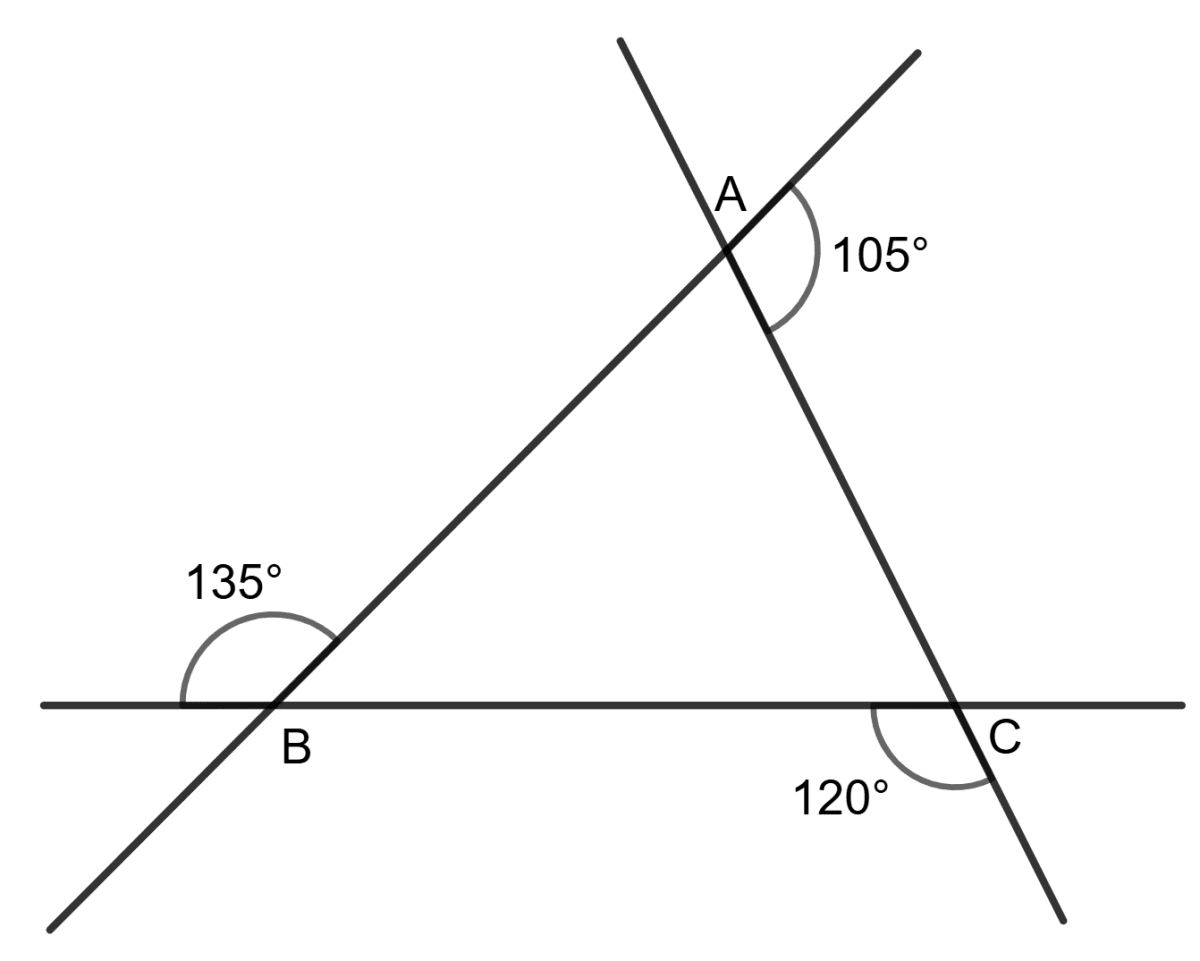
Reason (R): In △ABC,
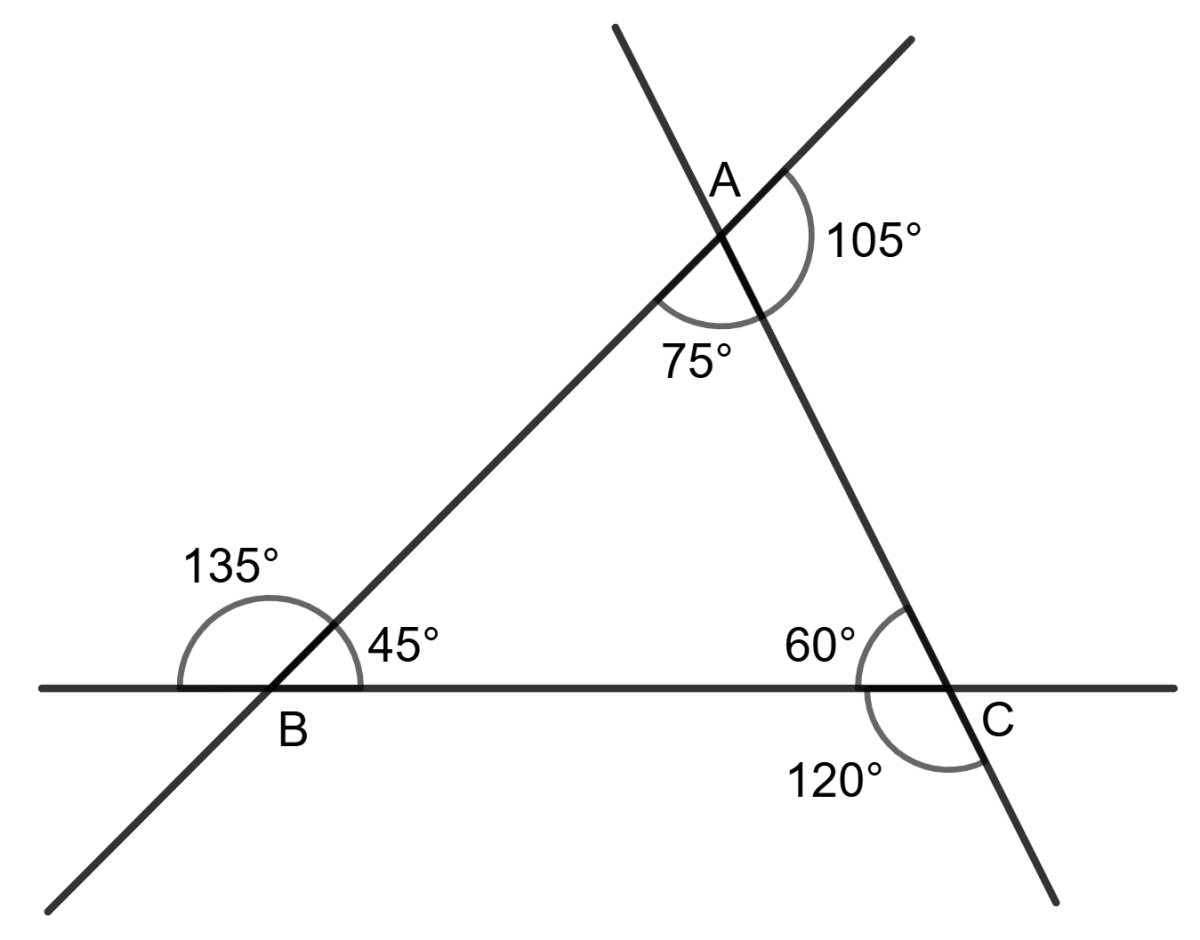
∠BAC > ∠ACB > ∠ABC
⇒ BC > AB > AC- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.