Mathematics
Assertion (A): Using the information in the given figure, we have PQ = 10 cm.
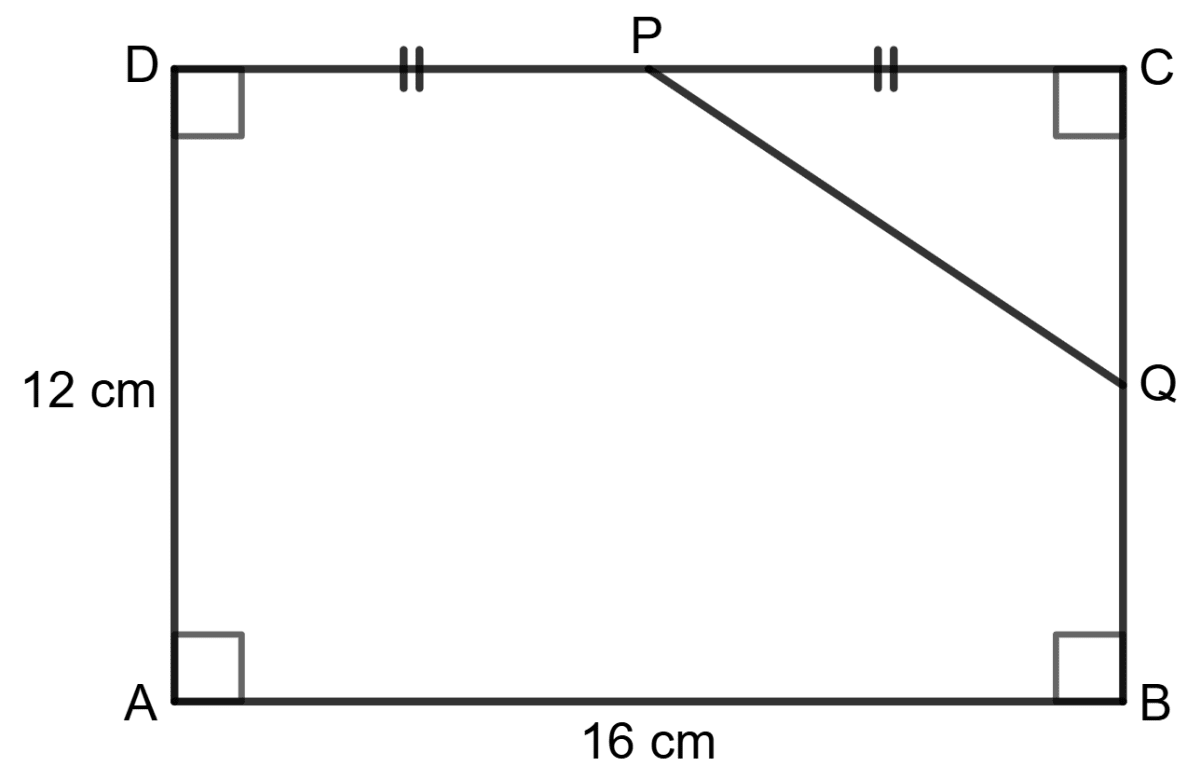
Reason (R): In right-triangle DAB, DB = 20 cm.

- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Mid-point Theorem
1 Like
Answer
Both A and R are true.
Explanation
Given,
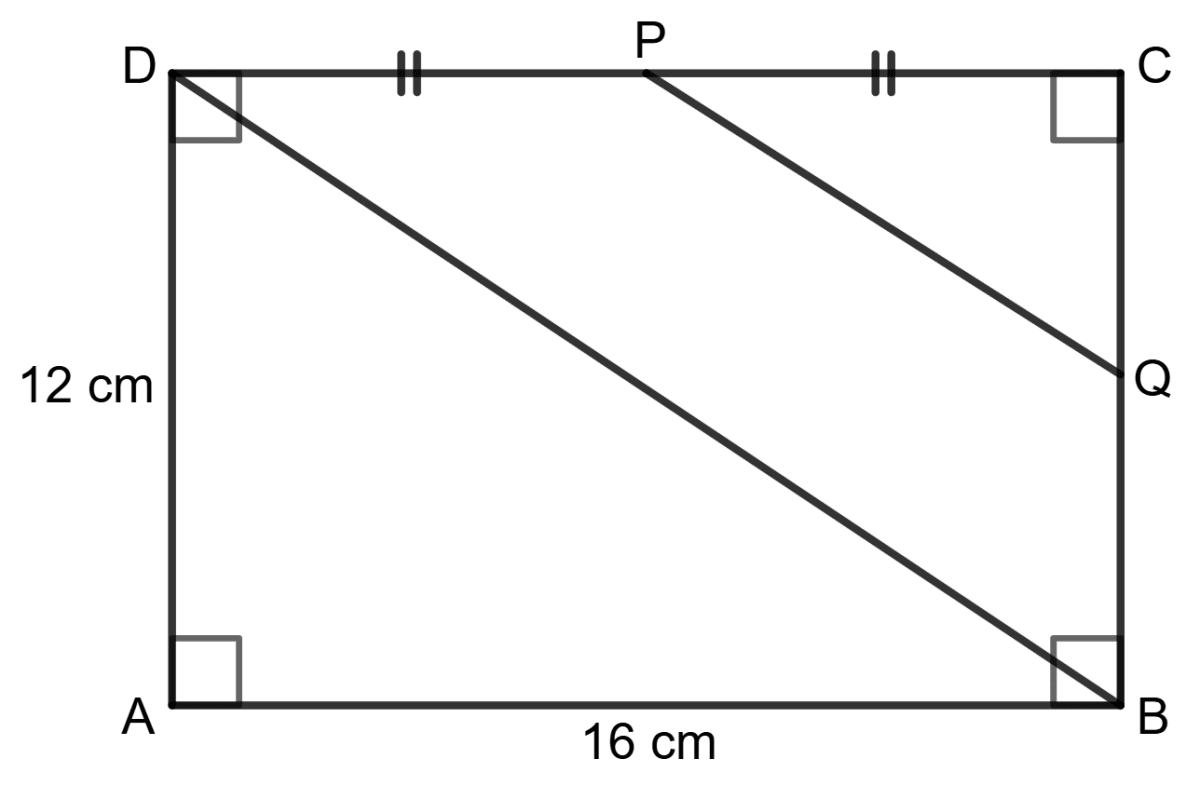
AB = 16 cm, AD = 12 cm
Using Pythagoras Theorem,
BD2 = AD2 + AB2
⇒ BD2 = 122 + 162
⇒ BD2 = 144 + 256
⇒ BD2 = 400
⇒ BD =
⇒ BD = 20 cm
Given, P is the mid point of DC.
Assuming Q as the mid point of BC,
In Δ BDC,
By mid-point theorem,
PQ // BD and
PQ = BD
∴ PQ = 20 = 10 cm
Hence, both Assertion (A) and Reason (R) are true.
Answered By
1 Like
Related Questions
Assertion (A): Using the information in the given figure, we get BC > AB > AC.
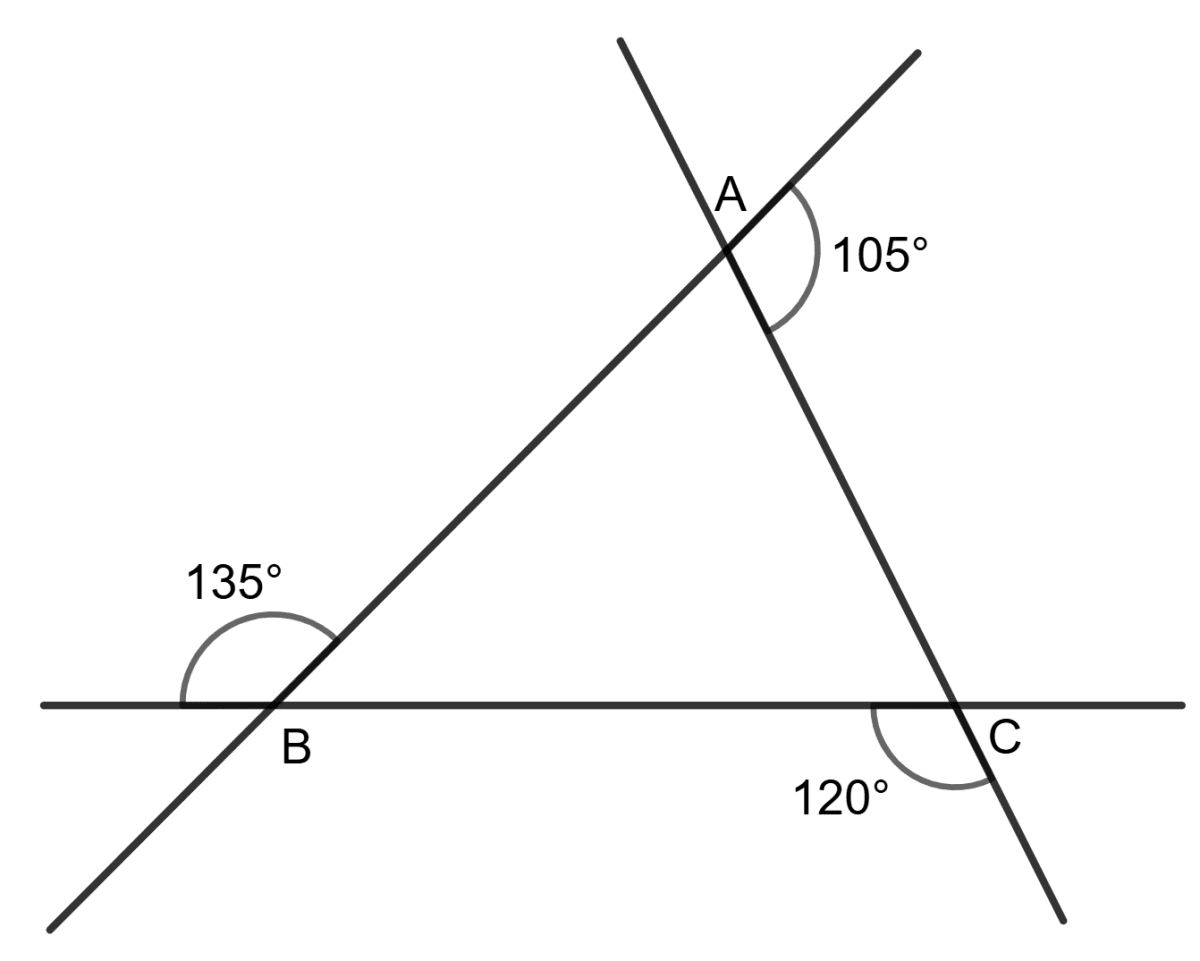
Reason (R): In △ABC,
∠BAC > ∠ACB > ∠ABC
⇒ BC > AB > AC- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): Using the information in the given figure, we get CE : EA = 5:3.
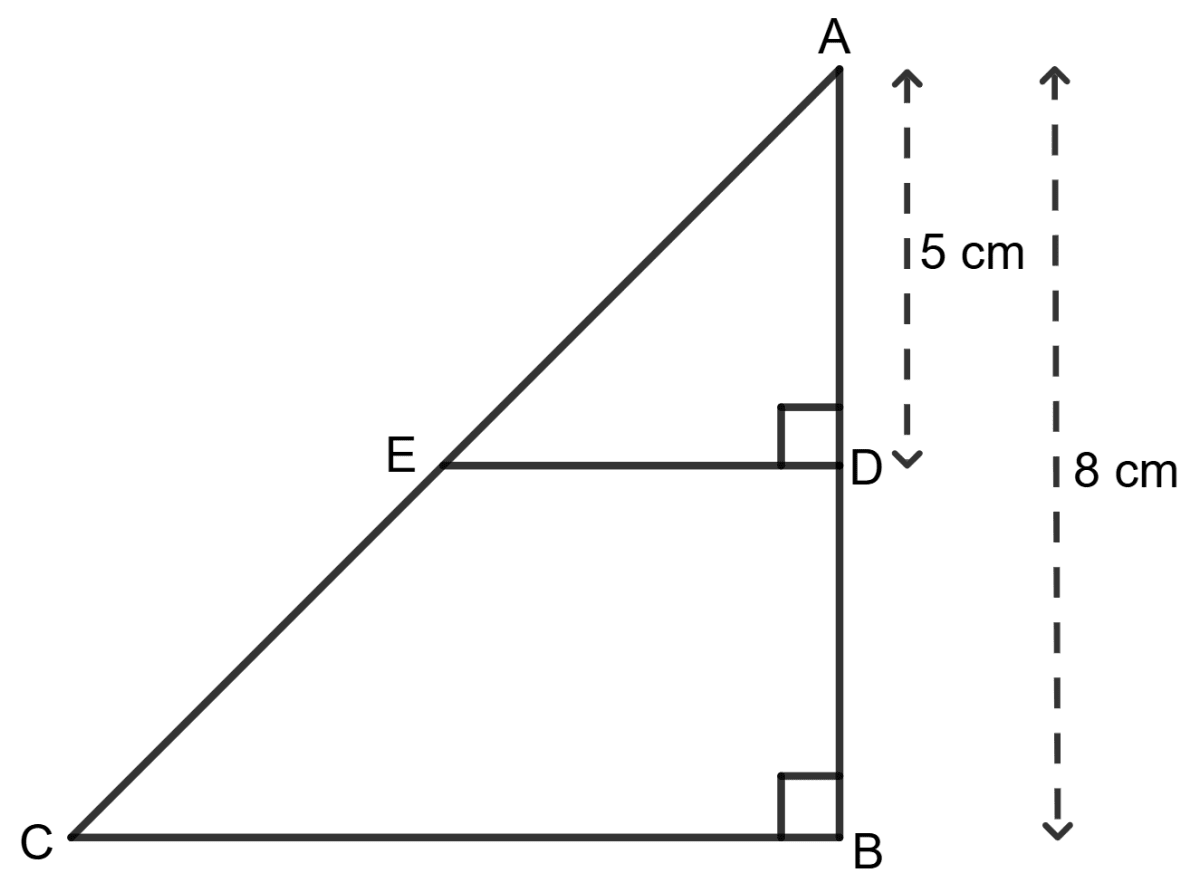
Reason (R): Since, ∠ADE = ∠ABC = 90°
so,
⇒ CE : EA = 3 : 5
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): From the information given in the figure, AP = 10 cm.
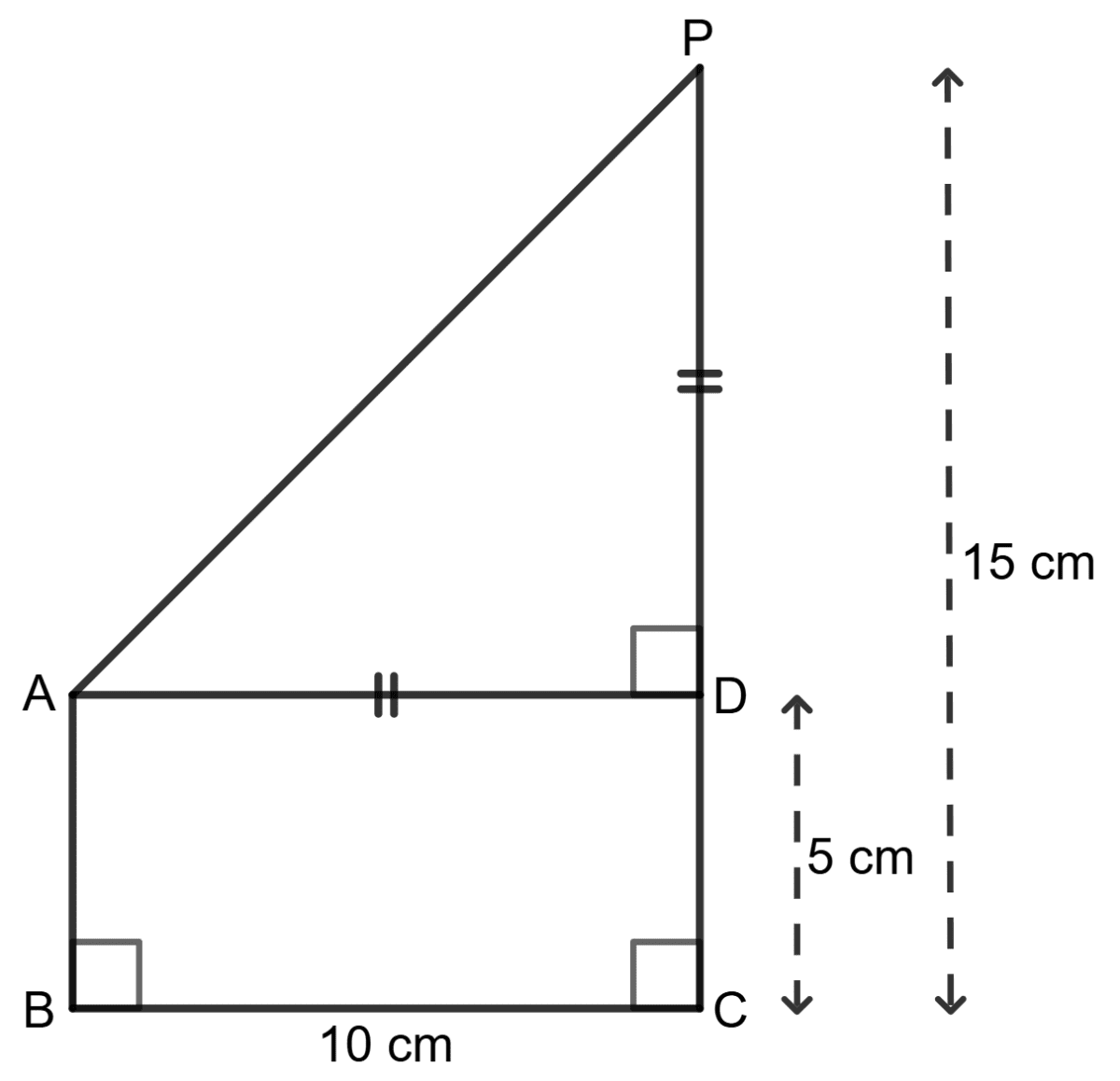
Reason (R):
⇒ AP2 = AD2 + DP2
⇒ AP2 = 102 + 102
AP =- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): According to the information in the given figure, the length of BC = 10 cm.

Reason (R):
∴ AB = AC - BC = 11 cm- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.