Mathematics
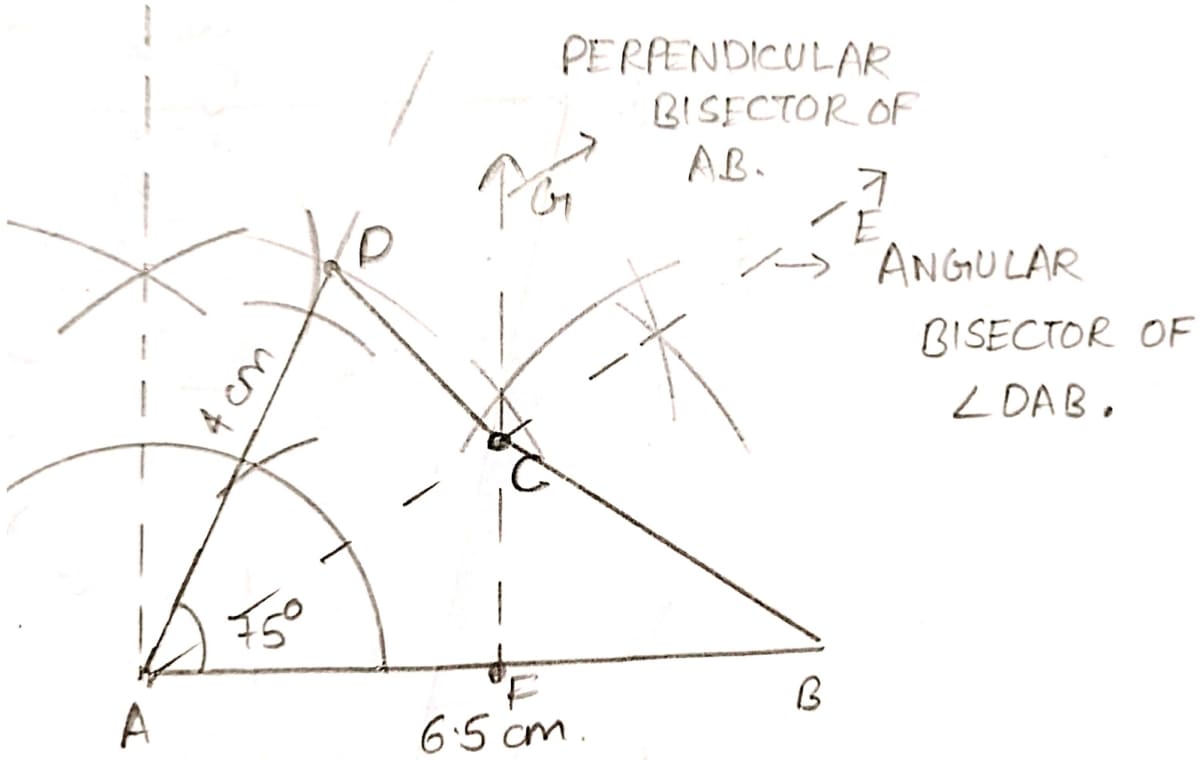
By using ruler and compasses only, construct a quadrilateral ABCD in which AB = 6.5 cm, AD = 4 cm and ∠DAB = 75°. C is equidistant from the sides AB and AD, also C is equidistant from the points A and B.
Locus
12 Likes
Answer
Steps of construction :
Draw AB = 6.5 cm as base.
At A, construct angle ∠DAB = 75° and cut an arc from A on it and mark point D such that AD = 4 cm.
Since, C is equidistant from the sides AB and AD, also C is equidistant from the points A and B hence it will be the intersection point of perpendicular bisector of AB i.e. FG and angle bisector of ∠DAB i.e. AE.
Join A, B, C and D forming quadrilateral ABCD.
Answered By
9 Likes
Related Questions
Two straight roads PQ and PK cross each other at P at an angle of 75°. S is a stone on the road PQ, 800 m from P towards Q. By drawing a figure to scale 1 cm = 100m, locate the position of a flag staff X, which is equidistant from P and S, and is also equidistant from the roads.
Construct a rhombus PQRS whose diagonals PR, QS are 8 cm and 6 cm respectively. Find by construction a point X equidistant from PQ, PS and equidistant from R, S. Measure XR.
Without using set square or protractor, construct the parallelogram ABCD in which AB = 5.1 cm, the diagonal AC = 5.6 cm and the diagonal BD = 7 cm. Locate the point P on DC, which is equidistant from AB and BC.
Use ruler and compass to answer this question. Construct ∠ABC = 90°, where AB = 6 cm, BC = 8 cm.
(a) Construct the locus of points equidistant from B and C.
(b) Construct the locus of points equidistant from A and B.
(c) Mark the point which satisfies both the conditions (a) and (b) as O. Construct the locus of points keeping a fixed distance OA from the fixed point O.
(d) Construct the locus of points which are equidistant from BA and BC.