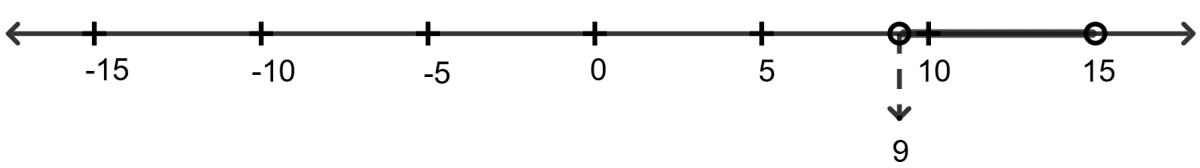Mathematics
Case Study I
Shivam's father is a building contractor. One day Shivam got his father’s measuring tape. He used it to find the dimensions of the kitchen garden in his home. He found that the length of the garden is one metre more than twice its breadth. He told his friend Akhil that the perimeter of the garden is more than or equal to 110 m and is less than or equal to 140 m.
Based on this information, answer the following questions:
1. If breadth of the garden is x m, then the algebraic representation of the given information is:
140 ≤ 6x + 2 ≤ 110, x ∈ R
110 ≤ 6x + 2 ≤ 140, x ∈ R
110 ≤ 4x + 2 ≤ 140, x ∈ R
110 ≤ 2x + 1 ≤ 140, x ∈ R
2. The solution set for the breadth of the garden is:
{x ∈ R : 18 ≤ x ≤ 23}
{x ∈ R : 16 ≤ x ≤ 24}
{x ∈ R : 18 ≤ x ≤ 24}
{x ∈ R : 20 ≤ x ≤ 28}
3. The greatest possible value of the breadth of the garden is:
18 m
20 m
22 m
23 m
4. What is the least possible length of the garden?
34 m
36 m
37 m
none of these
5. What is the greatest possible length of the garden?
47 m
51 m
46 m
none of these
Linear Inequations
1 Like
Answer
1. The breadth of garden is x m. Length = 2x + 1
By formula,
Perimeter of garden = P = 2(L + B)
= 2[(2x + 1) + x]
= (3x + 1) × 2
= 6x + 2
Given,
The perimeter of the garden is more than or equal to 110 m and is less than or equal to 140 m.
∴ 110 ≤ 6x + 2 ≤ 140
Hence, Option 2 is the correct option.
2. Solving
⇒ 110 ≤ 6x + 2 ≤ 140
Solving L.H.S of inequation,
⇒ 110 ≤ 6x + 2
⇒ 6x + 2 ≥ 110
⇒ 6x ≥ 110 - 2
⇒ 6x ≥ 108
⇒ x ≥
⇒ x ≥ 18 ………..(1)
Solving R.H.S of inequation,
⇒ 6x + 2 ≤ 140
⇒ 6x ≤ 140 - 2
⇒ 6x ≤ 138
⇒ x ≤
⇒ x ≤ 23. ……….(2)
From (1) and (2) we get,
∴ 18 ≤ x ≤ 23
Since x ∈ R,
Solution set = {x ∈ R : 18 ≤ x ≤ 23}
Hence, Option 1 is the correct option.
3. Greatest possible value of the breadth of garden is the maximum value in the interval : 18 ≤ x ≤ 23 that is 23 m.
Hence, Option 4 is the correct option.
4. Least possible value of the breadth of garden is the minimum value in the interval : 18 ≤ x ≤ 23 that is 18.
Length = 2x + 1
Least possible value of length of garden will be if x = 18,
Length = 2(18) + 1 = 36 + 1 = 37.
The least possible length of the garden is 37 m.
Hence, Option 3 is the correct option.
5. Greatest possible value of the breadth of garden is 23 m.
Length = 2x + 1
= 2(23) + 1
= 46 + 1
= 47 m.
The Greatest possible length of the garden is 47 m.
Hence, Option 1 is the correct option.
Answered By
3 Likes
Related Questions
Find the greatest integer which is such that if 7 is added to its double, then the resulting number is greater than three times the integer.
7
8
6
none of these
The solution set for the inequation 2x + 4 ≤ 14, x ∈ W is :
{1, 2, 3, 4, 5}
{0, 1, 2, 3, 4, 5}
{1, 2, 3, 4}
{0, 1, 2, 3, 4}
Case Study II
A few countries such as the USA officially use Fahrenheit as a unit for measuring temperature. Other countries prefer Celsius over Fahrenheit. The two different scales are related by the linear equation, . A scientist wants to store an experimental solution between a temperature range of 68°F and 77°F.
Based on the above information, answer the following questions:
1. The algebraic representation of the given information in degree Celsius is :
68 < + 32 ≤ 77, C ∈ R
68 ≤ − 32 ≤ 77, C ∈ R
68 ≤ − 32 < 77, C ∈ R
68 < + 32 < 77, C ∈ R
2. The solution set for the temperature in degree Celsius is:
{C ∈ R : 18 < C < 23}
{C ∈ R : 20 < C < 25}
{C ∈ R : 22 < C < 27}
{C ∈ R : 25 < C < 30}
3. What is the range of the temperature in degree Celsius?
between 20°C and 25°C
between 25°C and 30°C
between 18°C and 23°C
between 22°C and 27°C
4. Which of the following is the graphical representation of the temperature in degree Celsius?
a.
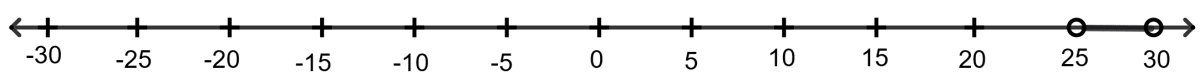
b.
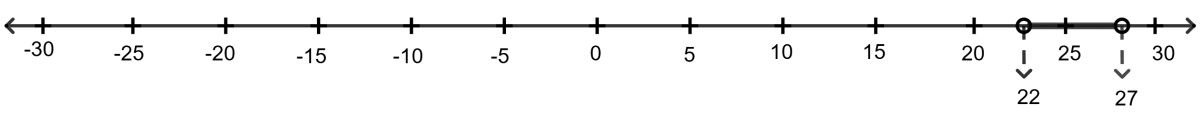
c.
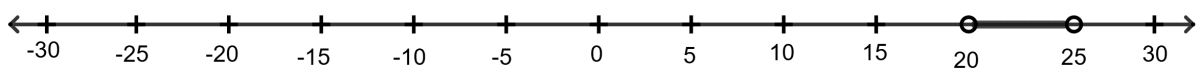
d.
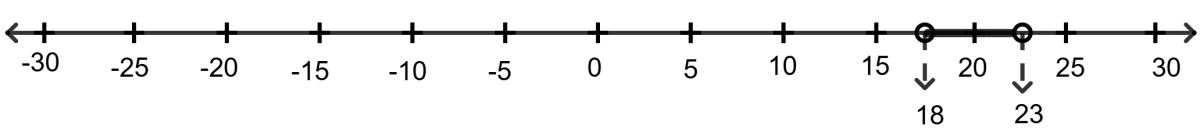
5. If the minimum temperature that can be maintained in a particular refrigerator is 0°C, what is the possible temperature range of the refrigerator on a Fahrenheit scale?
F >
F <
F > 32
F < 32
Case Study III
In drilling world’s deepest hole, the Kola Superdeep Borehole, the deepest man made hole on the earth, it was found that the temperature T in degree Celsius, x km below the earth’s surface was given by, T = 30 + 25(x - 3) and 3 ≤ x ≤ 15. If the temperature lies between 180° C to 330° C, then based on this information, answer the following questions.
1. The linear inequation for the depth of the hole is:
180 < 30 + 25(x − 3) < 330
180 ≤ 30 + 25(x − 3) ≤ 330
330 < 30 + 25(x − 3) ≤ 180
330 < 30 + 25(x − 3) < 180
2. The solution set for the depth is :
{x ∈ R : 6 ≤ x ≤ 12}
{x ∈ R : 9 ≤ x ≤ 12}
{x ∈ R : 3 ≤ x ≤ 15}
{x ∈ R : 9 ≤ x ≤ 15}
3. The minimum possible depth of the hole for the given temperature range is:
3 km
6 km
9 km
cannot be determined
4. The maximum possible depth of the hole for the given temperature range is:
9 km
12 km
15 km
None of these
5. Which of the following is the graphical representation of the solution set for the depth of the hole for the given temperature range?
a.
b.
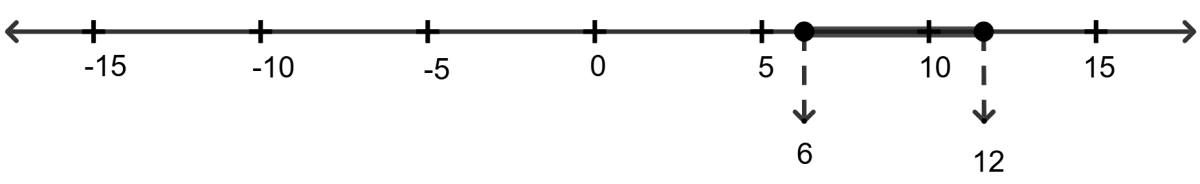
c.
d.