Mathematics
Consider the following two statements:
Statement 1: The line segment joining the mid-points of a pair of opposite sides of a parallelogram divides it into two equal parallelograms.
Statement 2: Diagonals of a parallelogram divide it into four triangles of equal area.
Which of the following is valid?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and Statement 2 is false.
Statement 1 is false, and Statement 2 is true.
Theorems on Area
1 Like
Answer
Let ABCD be a parallelogram in which E and F are mid-points of AB and CD respectively. Join EF.
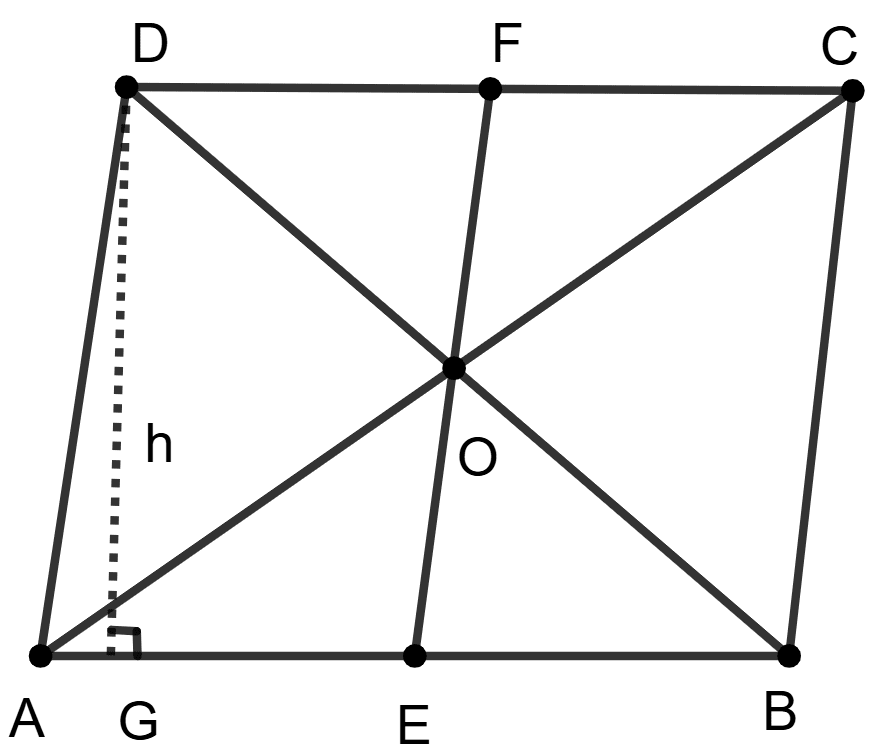
Let us construct DG ⊥ AB and let DG = h, where h is the altitude on side AB.
Area of || gm ABCD = base × height = AB × h
Area of ||gm AEFD = AE × h = × h ……………….(1) [Since E is the mid-point of AB]
Area of ||gm EBCF = EB × h = × h ……………….(2) [Since E is the mid-point of AB]
From (1) and (2),
Area of || gm AEFD = Area of || gm EBCF.
Thus, the line segment joining the mid-points of a pair of opposite sides of a parallelogram divides it into two equal parallelograms.
∴ Statement 1 is true.
From figure,
The diagonals AC and BD cut at point O.
In parallelogram, the diagonals bisect each other.
∴ AO = OC
In ∆ACD, O is the mid-point of AC.
∴ OD is the median.
Area of ∆AOD = Area of ∆COD …………….. (3) [Median of ∆ divides it into two triangles of equal areas.]
Similarly, in ∆ABC
O is the mid-point of AC.
∴ OB is the median.
Area of ∆AOB = Area of ∆COB …………….. (4) [Median of ∆ divides it into two triangles of equal areas.]
In ∆ADB,
O is the mid-point of BD.
∴ OA is the median.
Area of ∆AOD = Area of ∆AOB …………….. (5)
From (3), (4) and (5) we get,
Area of ∆AOB = Area of ∆COB = Area of ∆COD = Area of ∆AOD
So proved, that the diagonals of a parallelogram divide it into four triangles of equal area.
∴ Statement 2 is true.
∴ Both the statements are true.
Hence, option 1 is the correct option.
Answered By
2 Likes
Related Questions
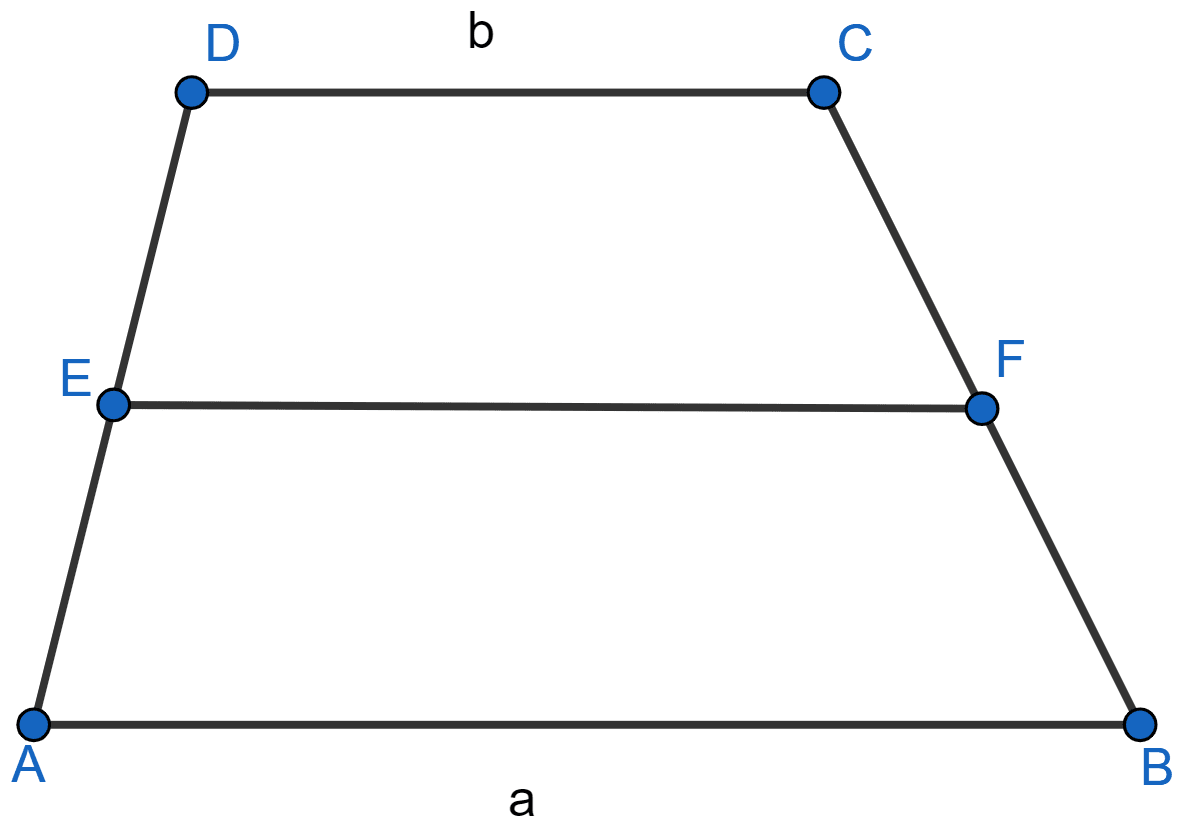
In the adjoining figure, ABCD is a trapezium with parallel sides AB = a cm and DC = b cm. E and F are mid-points of the non-parallel sides. The ratio of area of ABFE and area of EFCD is
a : b
(3a + b) : (a + 3b)
(a + 3b) : (3a + b)
(2a + b) : (3a + b)
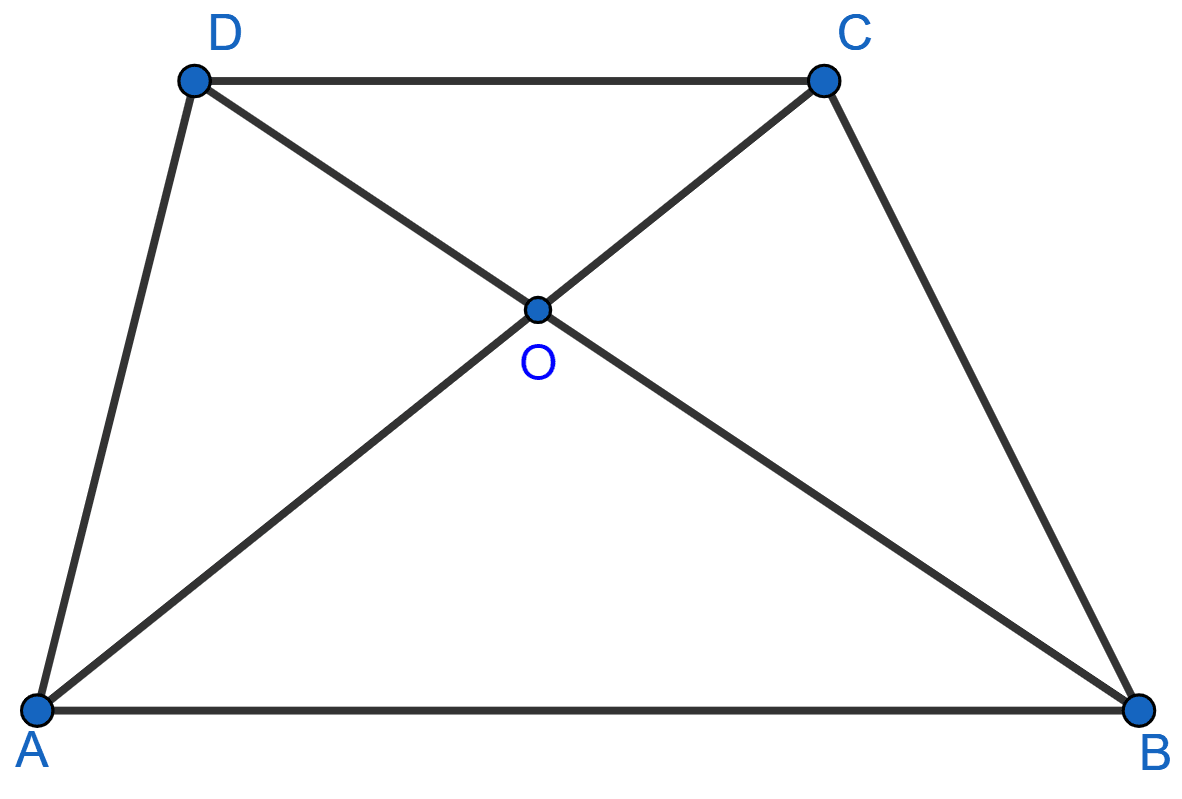
In the adjoining figure, AB || DC and AB ≠ DC. If the diagonals AC and BD of the trapezium ABCD intersect at O, then which of the following statements is not true ?
area of △ABC = area of △ABD
area of △ACD = area of △BCD
area of △OAB = area of △OCD
area of △OAD = area of △OBC
Assertion (A): Area of trapezium = (sum of parallel sides) x height.
Reason (R): A parallelogram and a rectangle on the same base and between the same parallel lines are equal in area.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
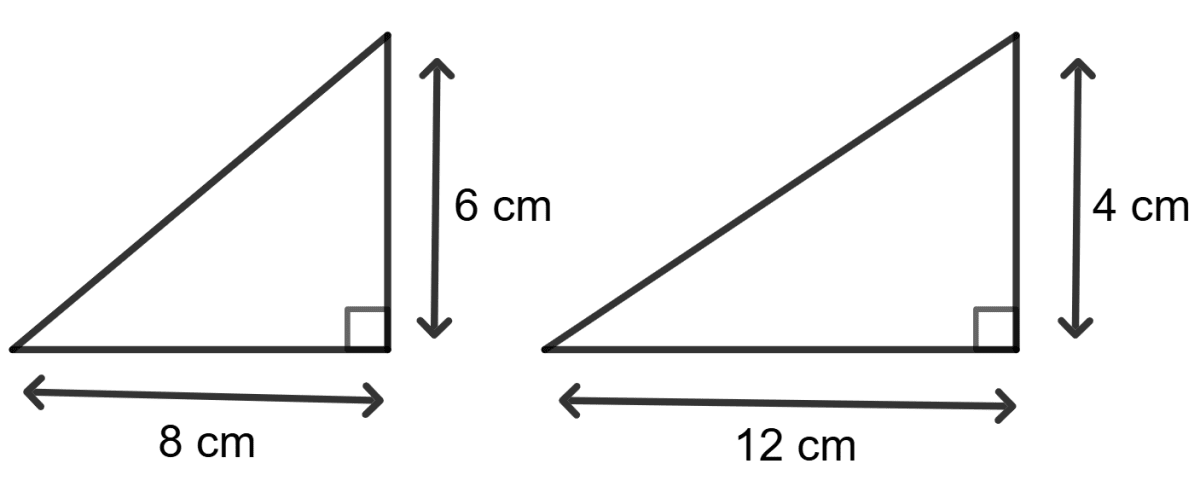
Assertion (A): In the adjoining figure, the two triangles are equal figures.
Reason (R): Two figures are called equal if and only if they have the same area.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).