Mathematics
Construct a △ABC with BC = 6.5 cm, AB = 5.5 cm, AC = 5 cm. Construct the incircle of the triangle. Measure and record the radius of the incircle.
Constructions
20 Likes
Answer
Steps of construction :
Draw a line segment BC = 6.5 cm.
Cut an arc from C of 5 cm and an arc of 5.5 cm from B.
Mark the point as A where the arcs from B and C intersect.
Join A, B and C. Hence, the △ABC is formed.
Draw the (internal) bisectors of ∠B and ∠C. Let these bisectors meet at point I.
From I, draw IN perpendicular to the side BC.
With I as centre and radius equal to IN, draw a circle. The circle so drawn touches all the sides of the △ABC, and is the required incircle of △ABC.
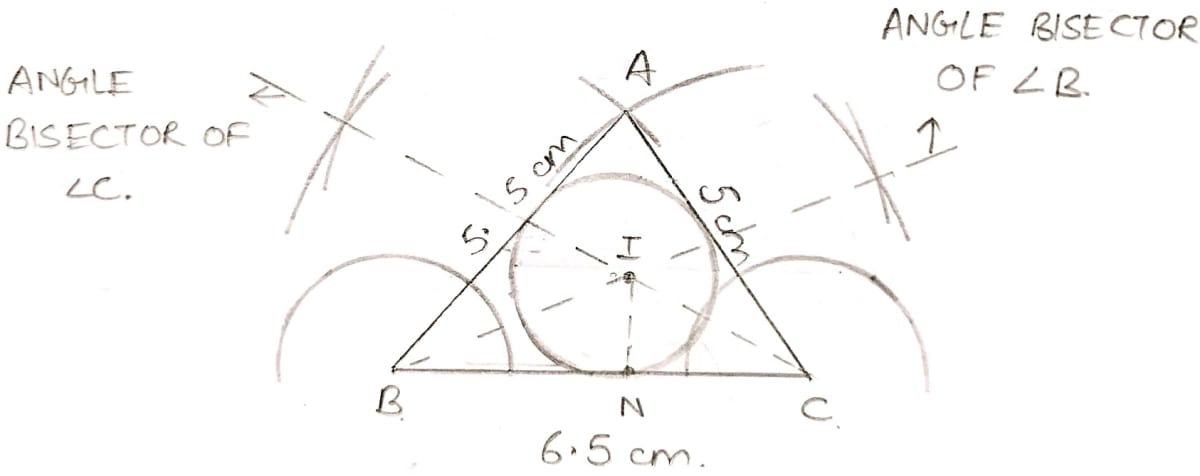
On measuring IN, we get the radius of the incircle.
Hence, the radius of incircle is 1.5 cm.
Answered By
16 Likes
Related Questions
Using ruler and compasses only, draw an equilateral triangle of side 5 cm and draw its inscribed circle. Measure the radius of the circle.
Construct a triangle ABC with BC = 6.4 cm, CA = 5.8 cm and ∠ABC = 60°. Draw its incircle. Measure and record the radius of incircle.
Using ruler and compasses only, construct a triangle ABC in which BC = 4 cm, ∠ACB = 45° and the perpendicular from A on BC is 2.5 cm. Draw the circumcircle of triangle ABC and measure its radius.
Using ruler and compasses only, construct a △ABC such that BC = 5 cm, AB = 6.5 cm and ∠ABC = 120°.
(i) Construct a circumcircle of △ABC.
(ii) Construct a cyclic quadrilateral ABCD such that D is equidistant from AB and BC.