A solid sphere with a radius of 4 cm is cut into 4 identical pieces by two mutually perpendicular planes passing through its center. Find the total surface area of one-quarter piece.

1. 24π

2. 32π

3. 48π

4. 64π

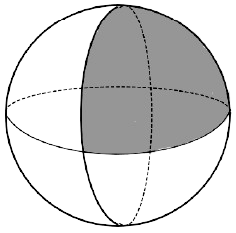
Two identical solid hemispheres are kept in contact to form a sphere. The ratio of the total surface areas of two hemispheres to the surface area of the sphere formed is :

1. 1 : 1

2. 3 : 2

3. 2 : 3

4. 2 : 1

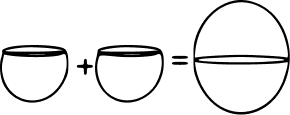
Given a = 3 sec² θ and b = 3 tan² θ - 2. The value of (a - b) is :

1. 1

2. 2

3. 3

4. 5

At a certain time of day, the ratio of the height of the pole to the length of its shadow is 1 : $\sqrt{3}$, then the angle of elevation of the sun at that time of the day is :

1. 30°

2. 45°

3. 60°

4. 90°