Physics
In the diagram below, four cones are depicted, each with a height of 12 cm. The position of the center of gravity is indicated by dots located at 9 cm, 8 cm, 4 cm, and 3 cm from the apex of each cone. Which of these cones is completely solid?

- 9 cm
- 8 cm
- 4 cm
- 3 cm
Force
10 Likes
Answer
9 cm
Reason — For a completely solid cone (of uniform density), the center of gravity (CG) lies at a height of one-fourth the height from the base.
Distance from apex = x Height
So, for a cone of height 12 cm,
This means that only the cone with CG at 9 cm from the apex behaves like a completely solid cone.
Answered By
6 Likes
Related Questions
The diagrams below show four pulley systems. State which of the statements following the diagrams is true.
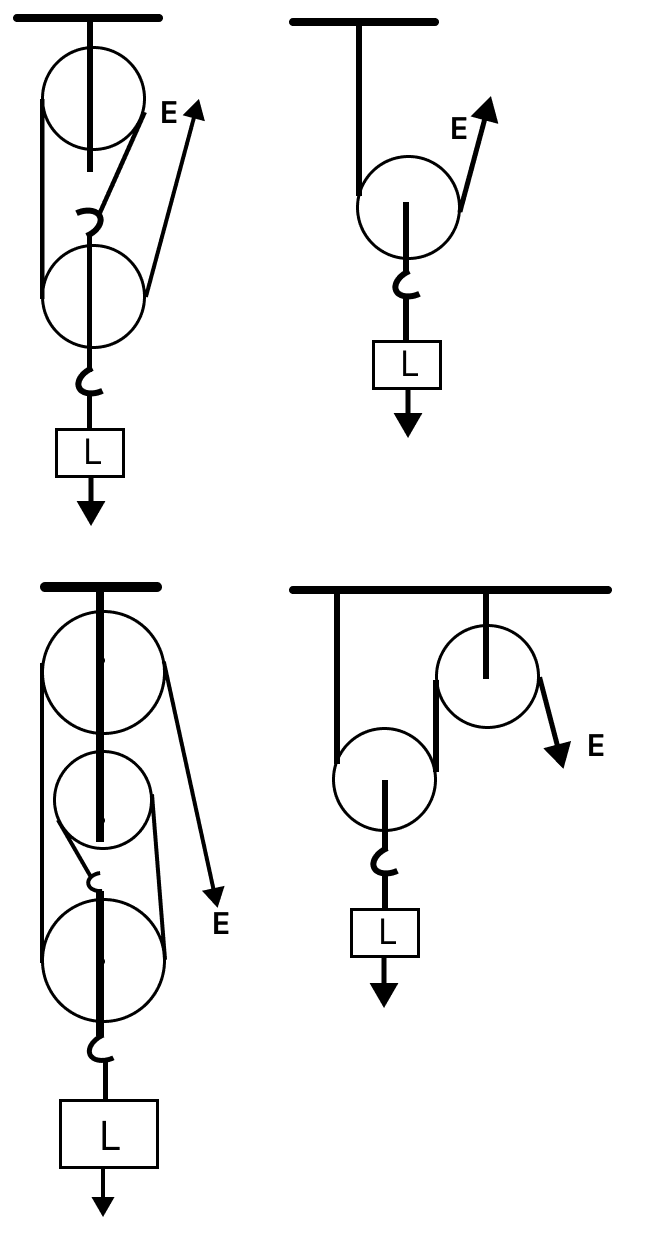
- There are three pulley systems with V.R. = 2 and one pulley system with V.R. = 1.
- There are two pulley systems with V.R. = 2, one pulley system with V.R. = 3 and one pulley system with V.R. = 1.
- There are two pulley systems with V.R. = 2, one pulley system with V.R.= 3 and one pulley system with V.R. = 4.
- There are two pulley systems with V.R. = 2 and two pulley system with V.R. = 3.
The diagrams below show a force F = 40 N acting on a rod AB pivoted at A in different directions. Identify the correct statement.
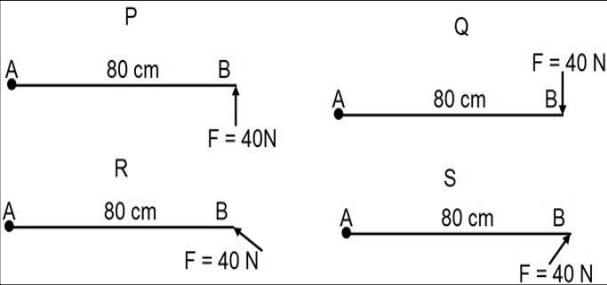
- P and S have opposite moments.
- The magnitude of the moment of force is maximum in R.
- The magnitude of the moment of force is maximum in P and Q.
- The moment of force in R is negative.
The given figure depicts the graph of work done vs. displacement under a constant force of 10 N. Which of the following statements is true?
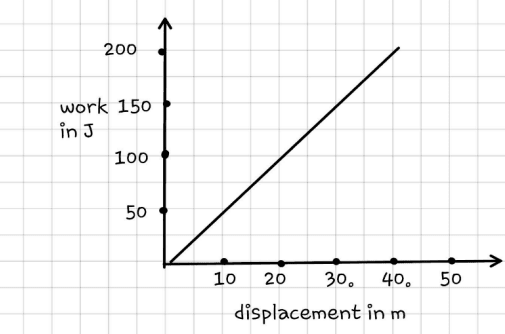
- Force is acting at an angle of 0° with the displacement.
- Force is acting at an angle of 45° with the displacement.
- Force is acting at an angle of 60° with the displacement.
- Force is acting at an angle of 90° with the displacement.
During his experiments with a single movable pulley, Jas determined the effort, mechanical advantage and efficiency as X, Y & Z, respectively. Subsequently, after lubricating the pulley thoroughly, he recalculated the effort, MA and efficiency. X', Y' & Z' respectively. Which of the following relationships accurately represents the scenario?
- X' > X
- Y' < Y
- Z' > Z
- Z' = Z