Mathematics
Draw and describe the locus in each of the following cases :
(i) The locus of vertices of all isosceles triangles having a common base.
(ii) The locus of points inside a circle and equidistant from two fixed points on the circle.
(iii) The locus of centres of all circles passing through two fixed points.
(iv) The locus of a point in rhombus ABCD which is equidistant from AB and AD.
Answer
(i) We know that,
The locus of point equidistant from two points is the perpendicular bisector of the line joining those points.
Steps of construction :
Draw a line segment BC (common base)
Draw XY, perpendicular bisector of BC.
Mark point P on XY.
So, PB = PC as P lies on perpendicular bisector of BC.
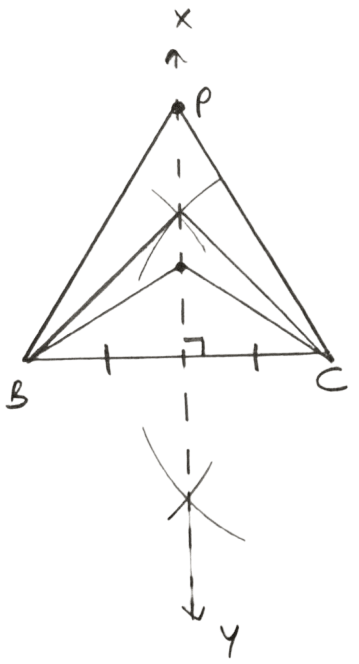
Hence, the locus of vertices of all isosceles triangles having a common base will be the perpendicular bisector of the common base of the triangles.
(ii) We know that,
The locus of point equidistant from two points is the perpendicular bisector of the line joining those points.
Steps of construction :
Construct a circle with center O.
Take two points A and B on the circle and join them.
Construct CD, perpendicular bisector of AB passing through center.
Mark point M and N on CD intersecting the circumference of the circle.

Hence, the locus of the points inside the circle which are equidistant from the fixed points on the circumference of a circle will be a diameter which is the perpendicular bisector of the line joining the two fixed points on the circle.
(iii) Let the two fixed points be A and B, and C1, C2, C3 be the centres of circles passing through A and B.
From figure we see that,
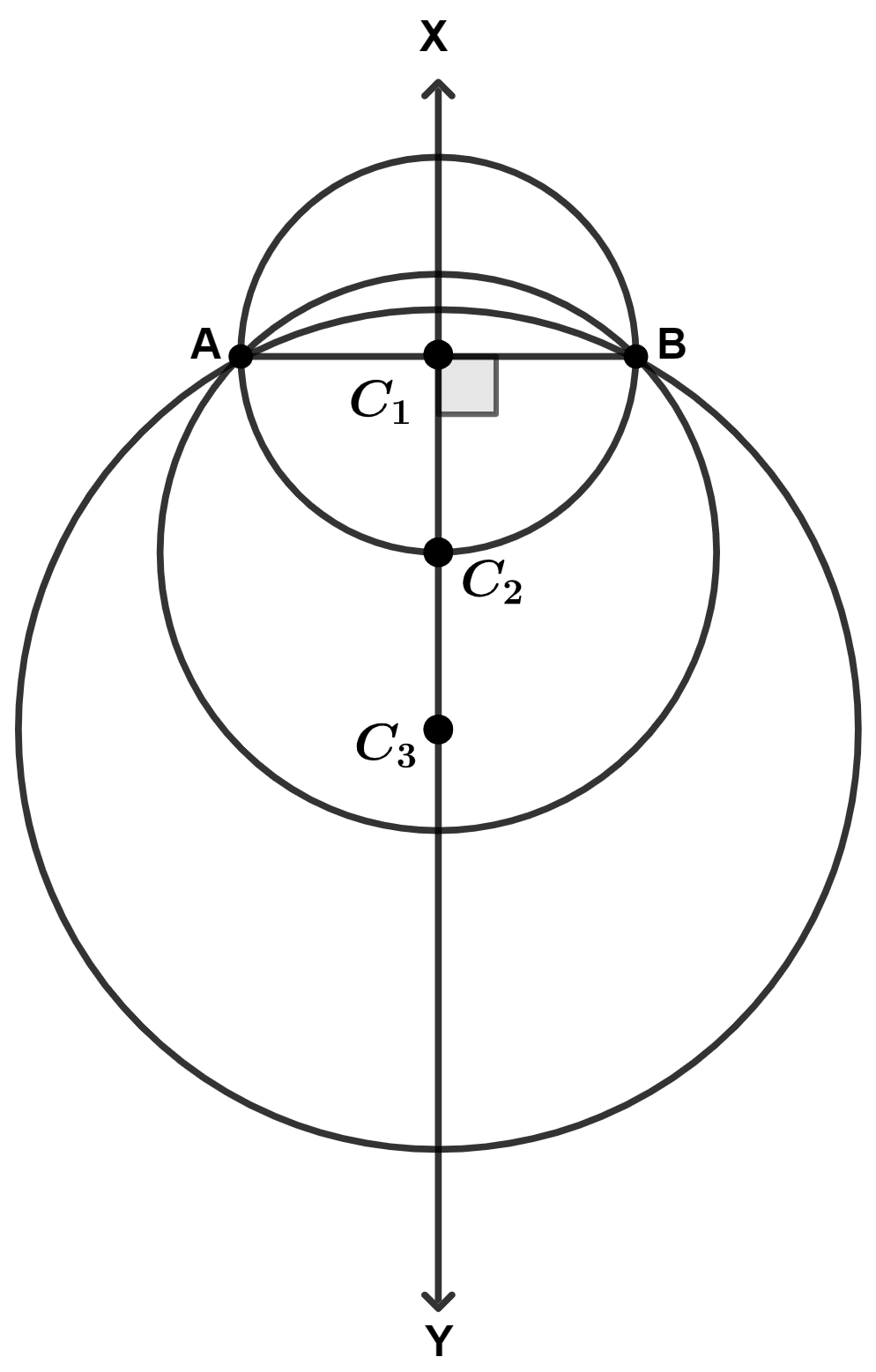
The locus of the centres of the circles passing through two points will be the perpendicular bisector of the line segment joining two fixed points.
(iv) We know that,
The locus of point equidistant from two sides is the angle bisector of the angle between the two lines.
Steps of construction :
Draw a rhombus ABCD.
Draw angle bisector of ∠A.
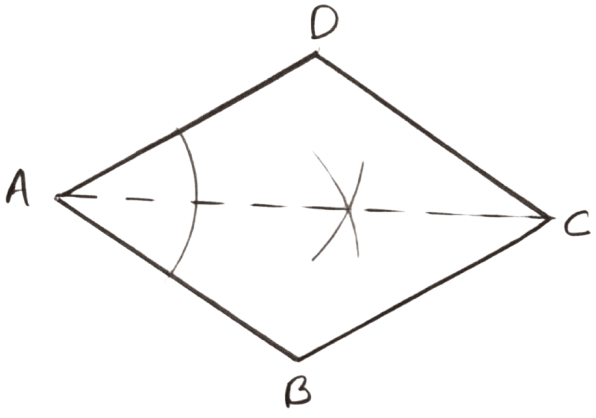
From figure,
Diagonal AC is the angle bisector of angle A.
Hence, required locus is the diagonal AC.
Related Questions
An express train makes a run of 240 km at a certain speed. Another train whose speed is 12 km/h less takes an hour longer to cover the same distance. Find the speed of the express train.
The expression 2x3 + ax2 + bx - 2 leaves remainders 0 and 7 when divided by (x + 2) and (2x - 3), respectively. Calculate the values of a and b. Factorise the expression completely.
A number m is randomly selected from the numbers 2, 3, 4 and then a number n is randomly selected from 1, 4, 9. What is the probability that the product of numbers m and n is less than 12?