Mathematics
Draw the graph of the straight line given by the equation 4x - 3y + 36 = 0
Calculate the area of the triangle formed by the line drawn and the co-ordinate axes.
Graphical Solution
16 Likes
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -9, then 4 (-9) - 3y + 36 = 0 ⇒ y = 0
Let x = -6, then 4 (-6) - 3y + 36 = 0 ⇒ y = 4
Let x = -3, then 4 (-3) - 3y + 36 = 0 ⇒ y = 8
Let x = 0, then 4 0 - 3y + 36 = 0 ⇒ y = 12
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -9 | -6 | -3 | 0 |
|---|---|---|---|---|
| y | 0 | 4 | 8 | 12 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
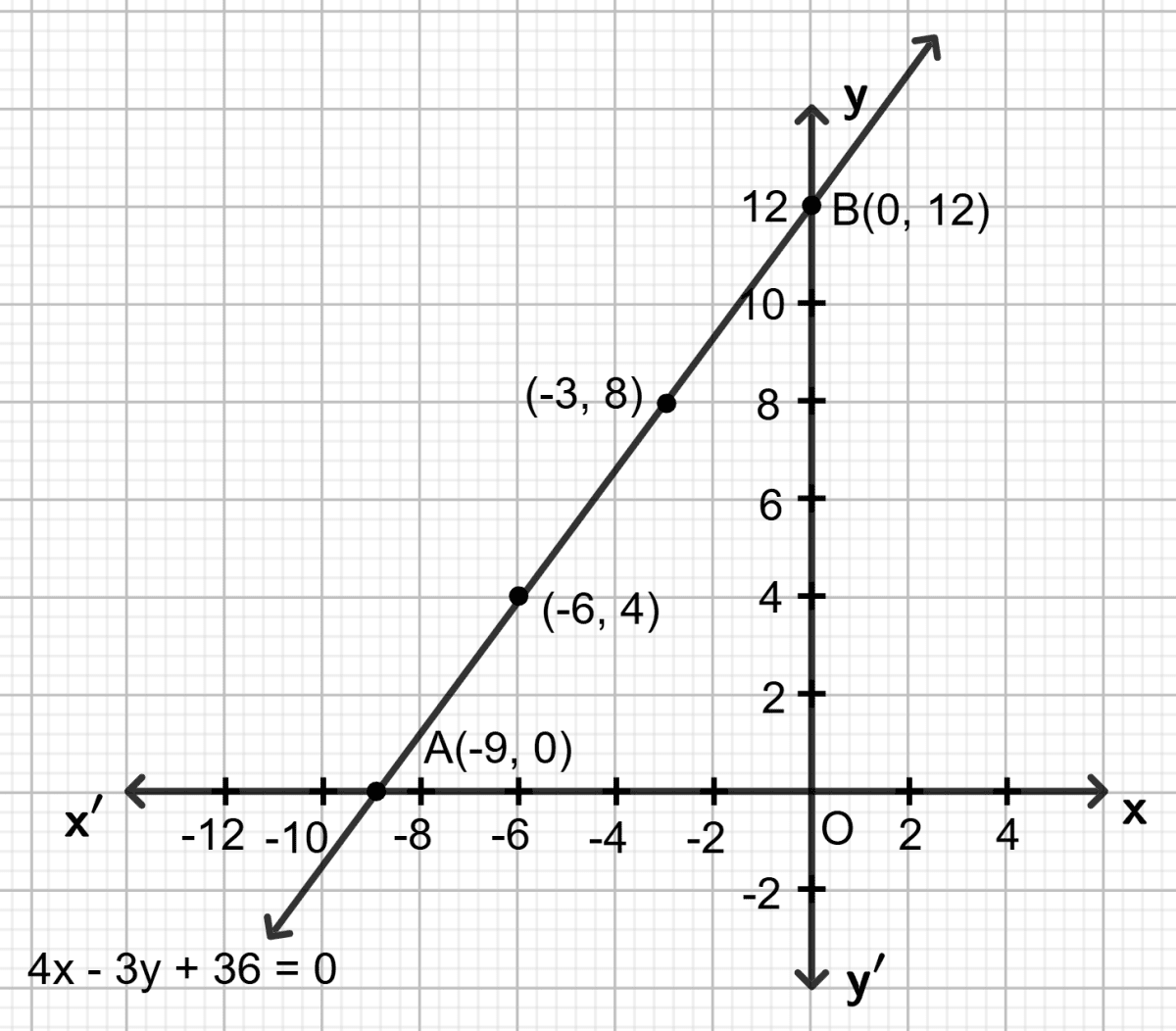
Area of triangle OAB = OA x OB
= x 9 x 12 square units
= x 108 square units
= 54 square units
Hence, area of triangle = 54 sq. units.
Answered By
9 Likes
Related Questions
Draw the graph for each equation, given below :
(i) x = 5
(ii) x + 5 = 0
(iii) y = 7
(iv) y + 7 = 0
(v) 2x + 3y = 0
(vi) 3x + 2y = 6
(vii) x - 5y + 4 = 0
(viii) 5x + y + 5 = 0
Draw the graph for each equation given below; hence find the co-ordinates of the points where the graph drawn meets the co-ordinate axes :
(i)
(ii)
Draw the graph of the equation
2x - 3y - 5 = 0
From the graph, find :
(i) x1, the value of x, when y = 7
(ii) x2, the value of x, when y = -5
Draw the graph of the equation
4x + 3y + 6 = 0
From the graph, find :
(i) y1, the value of y, when x = 12
(ii) y2, the value of y, when x = -6