Draw the necessary diagram for this question.

A man on the top of a lighthouse observes the angle of depression of two ships on the opposite sides of the lighthouse as 30° and 50° respectively. If the height of the lighthouse is 80 m, find the distance between the two ships.

Give your answer correct to the nearest meter.

From figure,

Let the top of the lighthouse be T, the base of the lighthouse be L, and the two ships be A and B.

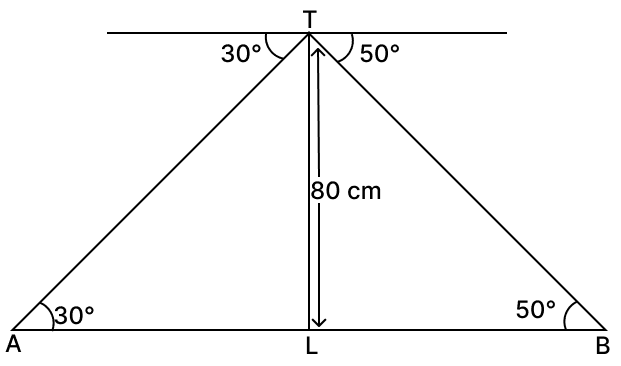
Given,

The height of the lighthouse, TL, is 80 m.

The angles of depression are 30° and 50°.

These are equal to the alternate interior angles of elevation at the ships.

∠TBL = 50° and ∠TAL = 30°

In triangle TLA,

$\Rightarrow \tan 30° = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow \tan 30° = \dfrac{TL}{LA} \\[1em] \Rightarrow LA = \dfrac{TL}{\tan 30°} \\[1em] \Rightarrow LA = \dfrac{80}{0.577} \\[1em] \Rightarrow LA = 138.65 \text{ m}.$

In triangle TLB,

$\Rightarrow \tan 50° = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow \tan 50° = \dfrac{TL}{LB} \\[1em] \Rightarrow LB = \dfrac{TL}{\tan 50°} \\[1em] \Rightarrow LB = \dfrac{80}{1.192} \\[1em] \Rightarrow LB = 67.11 \text{ m}.$

Distance between ships = LA + LB

= 138.65 m + 67.11 m = 205.76 m.

Hence, the distance between the two ships is 206 m.