Science
An electric heater consists of three similar heating elements A, B and C, connected as shown in the figure below. Each heating element is rated as 1.2 kW, 240 V and has constant resistance. S1, S2 and S3 are respective switches.
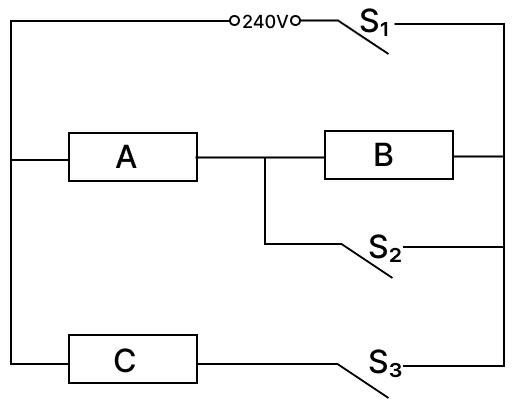
The circuit is connected to a 240 V supply.
(a) Calculate the resistance of one heating element.
(b) Calculate the current in each resistor when only S1 and S3 are closed.
(c) Calculate the power dissipated across A when S1, S2 and S3 are closed.
Current Electricity
6 Likes
Answer
Given,
- Power rating of each heater () = 1.2 kW = 1.2 x 1000 W = 1200 W
- Voltage rating of the heater () = Voltage supply = 240 V
(a) Resistance of one heating element is given by,
Hence, the resistance of one heating element is 48 Ω
(b) When S1 and S3 are closed then heating elements A and B are in series and this whole arrangement is in parallel combination with C.
Then,
Potential difference across A and B = Potential difference across C = 240 V
Now,
Since A and B are connected in series then their effective resistance is given by,
Then,
Hence, current through heating elements A nd B is 2.5 A and through C is 5 A.
(c) When S1, S2 and S3 are closed then current only flows through A but no current flows through B since current takes path of minimum resistance.
So elements A and C are in parallel and have same resistance it means current flowing through them will be equal.
Current through A = Current through C = 5 A
Then,
Hence, power dissipated across A is 1200 W.
Answered By
4 Likes
Related Questions
Zarina worked as an apprentice in a factory where flashlights and solar cookers are made. She learnt to make the circuits, the design of the light-box and light concentrators of the solar cookers as well. She learnt the uses of lenses in making all those tools. Based on your understanding of lenses, answer the following questions.
(a) What kind of lenses are used in the flashlight and light concentrator of the solar-cooker?
(b) Give reasons for your choices in your answer for part A.
Attempt either subpart C or D.
(c) An object is placed 40 cm away from a lens which is normally used in a solar-cooker. The image formed is twice the size of the object. Calculate the focal length of the lens.
OR
(d) An object is placed 20 cm in front of a lens which is used in a flashlight, and the image is formed 10 cm away from the lens on the same side as the object. Calculate the focal length of the lens.
The arrangement of resistors shown in the below figure is connected to a battery.

The power dissipation in the 100 Ω resistor is 81 W. Calculate
(a) the current in the circuit
(b) the reading in the voltmeter V2
(c) the reading in the voltmeter V1
(a) Explain why in household circuits only the fuse is connected in series with all the rest of the appliances but all appliances are connected in parallel to each other.
(b) In a household circuit, an electric heater of power 1500 W and a fan of power 500 W are connected in parallel to a 220 V supply. A fuse rated for 10 A is connected to the circuit to protect it from excessive current.
- Calculate the total current drawn by the heater and the fan.
- Determine whether the 10 A fuse is appropriate for this circuit or if it will blow.
Two resistors, R1 = 6 Ω and R2 = 12 Ω, are connected in parallel to a 24 V battery. The circuit operates for 5 minutes.
(a) Calculate the total heat generated in both resistors.
(b) If each resistor has a power rating of 100 W, determine whether it is safe to use these resistors in the circuit.