Find the area of a triangle whose sides are 18 cm, 24 cm and 30 cm.

Also, find the length of altitude corresponding to the largest side of the triangle.

Let the sides of the triangle be:

a = 18 cm, b = 24 cm and c = 30 cm.

The semi-perimeter s:

$∵ s = \dfrac{a + b + c}{2}\\[1em] = \dfrac{18 + 24 + 30}{2}\\[1em] = \dfrac{72}{2}\\[1em] = 36$

∵ Area of triangle = $\sqrt{s(s - a)(s - b)(s - c)}$

= $\sqrt{36(36 - 18)(36 - 24)(36 - 30)}$ cm²

= $\sqrt{36 \times 18 \times 12 \times 6}$ cm²

= $\sqrt{46,656}$ cm²

= 216 cm²

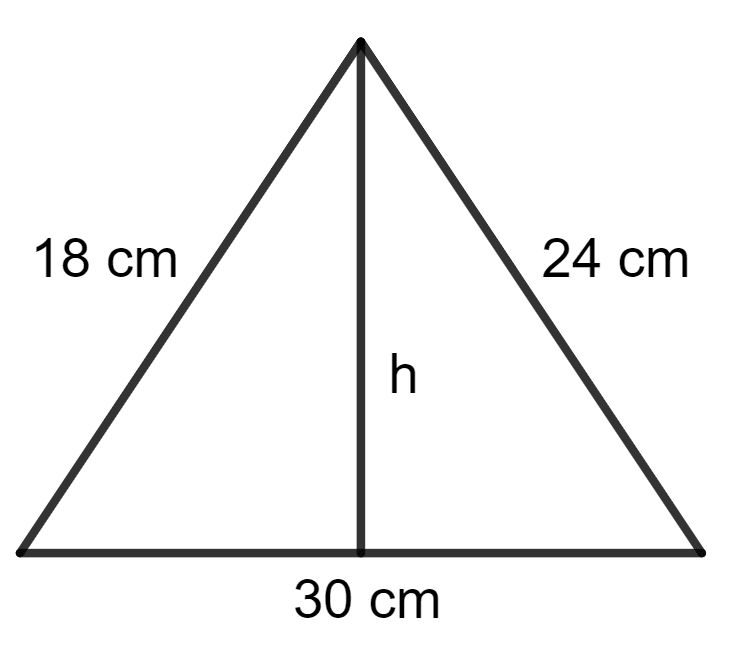
Using the area formula to find the altitude corresponding to the largest side (base = 30 cm):

Area = $\dfrac{1}{2}$ x base x altitude

Let h be the altitude:

⇒ 216 = $\dfrac{1}{2}$ x 30 x h

⇒ 216 = 15 x h

⇒ h = $\dfrac{216}{15}$

⇒ h = 14.4 cm

Hence, the area of the triangle is 216 cm² and the length of altitude corresponding to the largest side is 14.4 cm.