Mathematics
Find the least number which must be added to 5483 so that the resulting number is a perfect square.
Sq & Sq Roots
7 Likes
Answer
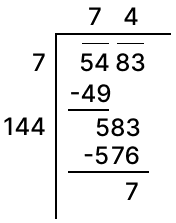
Clearly, 5483 is greater than 742.
∴ On adding the required number to 5483, we shall be getting 752 i.e, 5625
So, the required number = 5625 - 5483 = 142.
Hence, 142 should be added to 5483.
Answered By
4 Likes
Related Questions
Find the least number which must be added to 1205 so that the resulting number is a perfect square.
Find the least number which must be subtracted from 2037 so that the resulting number is a perfect square.
The value of 182 - 172 is :
1
-1
35
none of the above
The sum of first four odd natural numbers is :
23
24
43
44