Mathematics
Find the value of cot x.
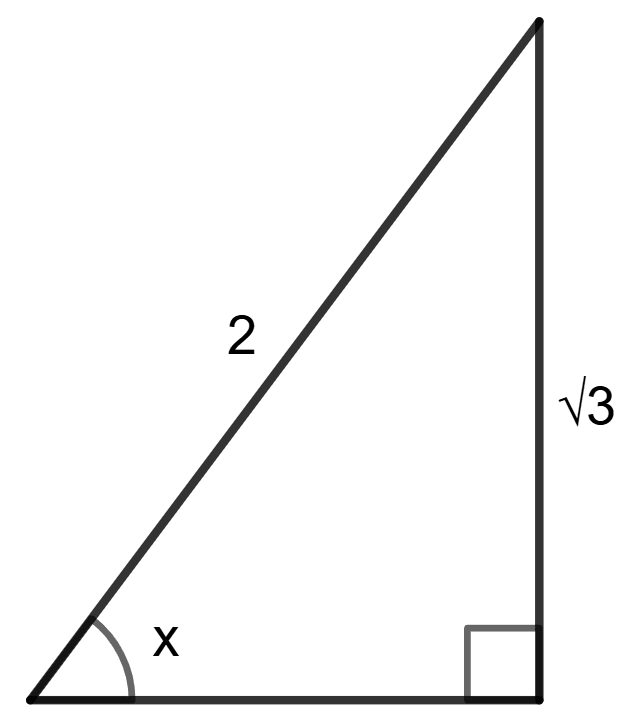
Trigonometric Identities
14 Likes
Answer
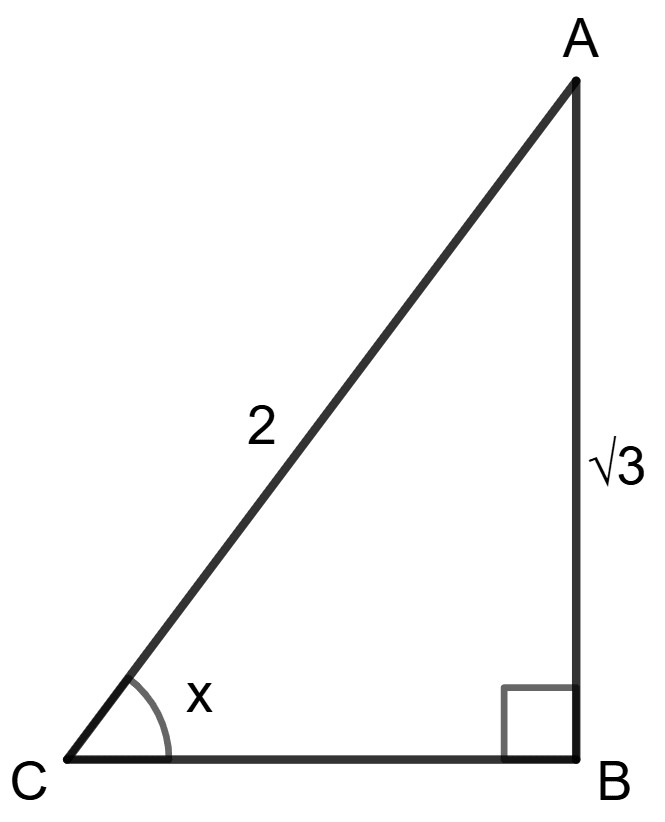
In Δ ABC, according to Pythagoras theorem,
⇒ AC2 = BC2 + AB2 (∵ AC is hypotenuse)
⇒ 22 = BC2 + ()2
⇒ 4 = BC2 + 3
⇒ BC2 = 4 - 3
⇒ BC2 = 1
⇒ BC =
⇒ BC = 1
Hence, cot x = .
Answered By
10 Likes
Related Questions
Assertion (A): In rhombus ABCD, angle ABC = 120° and length of its each side is 20 cm. The length of diagonal BD = 20 cm.
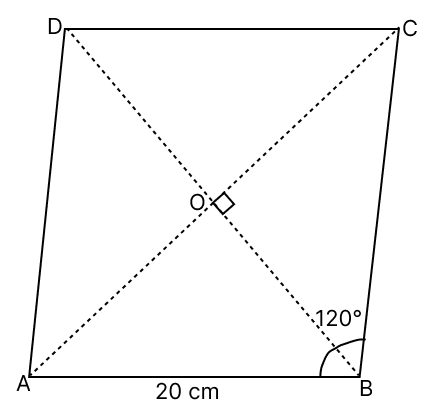
Reason (R): In ΔAOB, cos 60° = and BD = 2 x OB
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Assertion (A): The length of the line AB is 100 m.
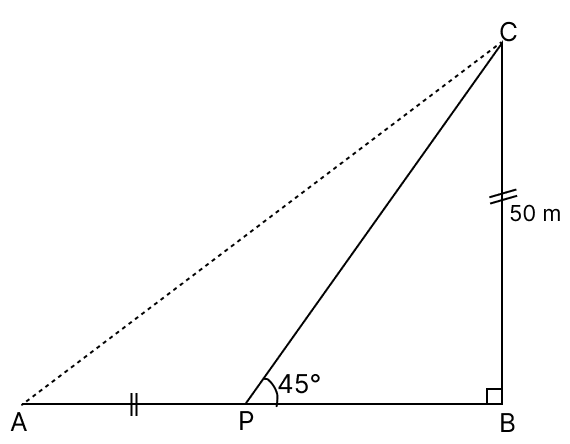
Reason (R): tan 45° = ⇒ PB = 50 m and AB = 50 m + 50 m = 100 m
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Find the length of AB.
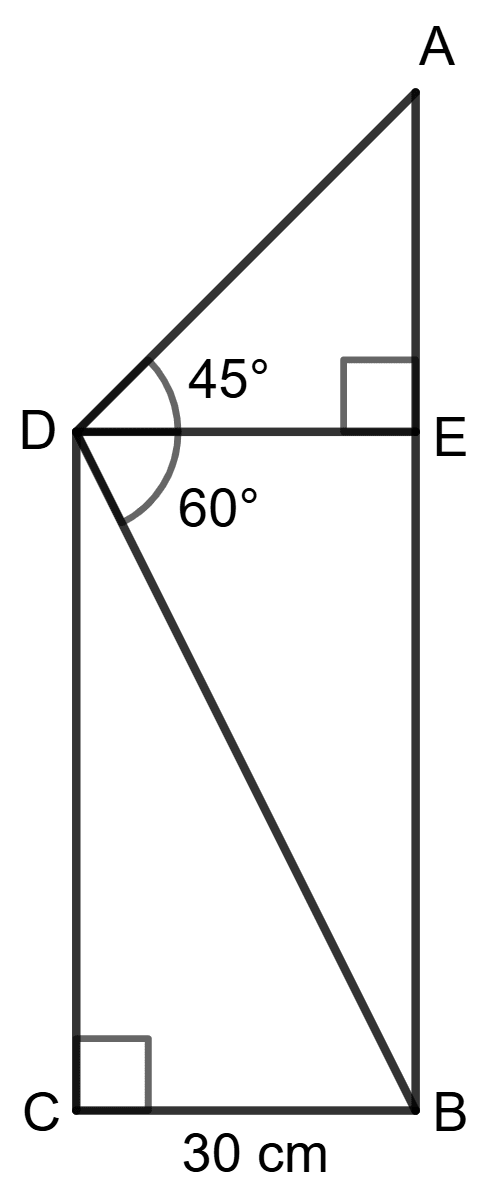
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.
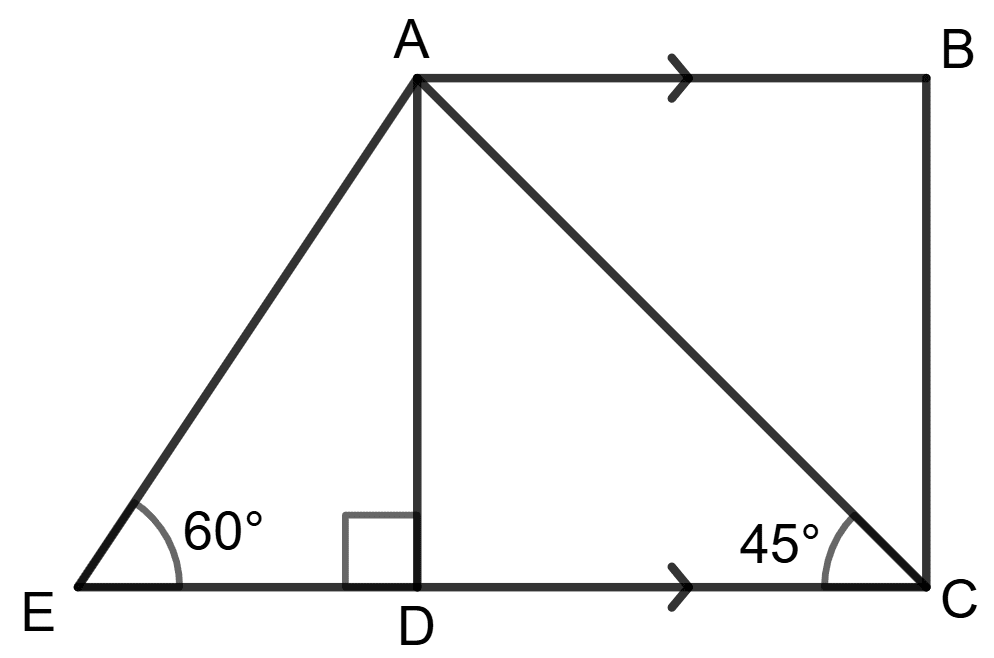
Given that ∠AED = 60° and ∠ACD = 45°; calculate :
(i) AB
(ii) AC
(iii) AE