Mathematics
The following figure shows a circle with center O and a diameter AB.

(i) Name the angle APB.
(ii) State the measure of angle APB.
(iii) If AP = 12 cm and OA = 10 cm; find the lengths of AB and BP.
(iv) If 4AP = 3PB = 12 cm; find the radius of the circle.
Circles
19 Likes
Answer
(i) AB is diameter of the circle.
Hence, angle APB is the angle of semi-circle.
(ii) As, the angle subtended by a diameter at any point on the circumference of a circle is a right angle (90°).
Hence, angle APB = 90°.
(iii) Given,
AP = 12 cm and OA = 10 cm
⇒ OA = OB (Radii of the circle)
⇒ OB = 10 cm
From figure,
⇒ AB = OA + OB = 10 cm + 10 cm = 20 cm
Since, angle APB = 90°.
Using pythagoras theorem,
⇒ AP2 + PB2 = AB2
⇒ 122 + PB2 = 202
⇒ 144 + PB2 = 400
⇒ PB2 = 400 - 144
⇒ PB2 = 256
⇒ PB =
⇒ PB = 16 cm.
Hence, AB = 20 cm and PB = 16 cm.
(iv) Given,
⇒ 4AP = 3PB = 12 cm
⇒ AP = = 3 cm
⇒ PB = = 4 cm
Since, angle APB = 90°.
Using pythagoras theorem,
⇒ AP2 + PB2 = AB2
⇒ 32 + 42 = AB2
⇒ 9 + 16 = AB2
⇒ 25 = AB2
⇒ AB =
⇒ AB = 5 cm
Now, OA = OB (Radii of the circle)
From figure,
⇒ AB = OA + OB
⇒ AB = 2 x OA
⇒ 5 = 2 x OA
⇒ OA = = 2.5 cm.
Hence, the radius of the circle = 2.5 cm.
Answered By
10 Likes
Related Questions
Fill in the blanks :
(i) An arc is the part of the ……………….
(ii) Diameter of a circle bisects …………
(iii) The part of the circumference greater than the semicircle is called …………….
(iv) Sector of a circle is its region bounded by ……………..
(v) The segment of a circle is the region bounded by ………………
(vi) A tangent of a circle meets the circle at …………..
(vii) The number of tangents that can be drawn through a point on its circumference = ……………
(viii) The number of tangent that can be drawn through a point outside the circle is ……………..
O is the center of a circle with diameter 30 cm. P is a point outside the circle and PA is tangent of the circle. Find :
(i) the length of tangent PA; if OP = 39 cm.
(ii) the distance between O and P, if the length of the tangent PA is 20 cm.
Find the length of the tangent to a circle with radius 5 cm, from a point at a distance of 13 cm from its center.
The following figure shows a circle with diameter AB and center at point O.
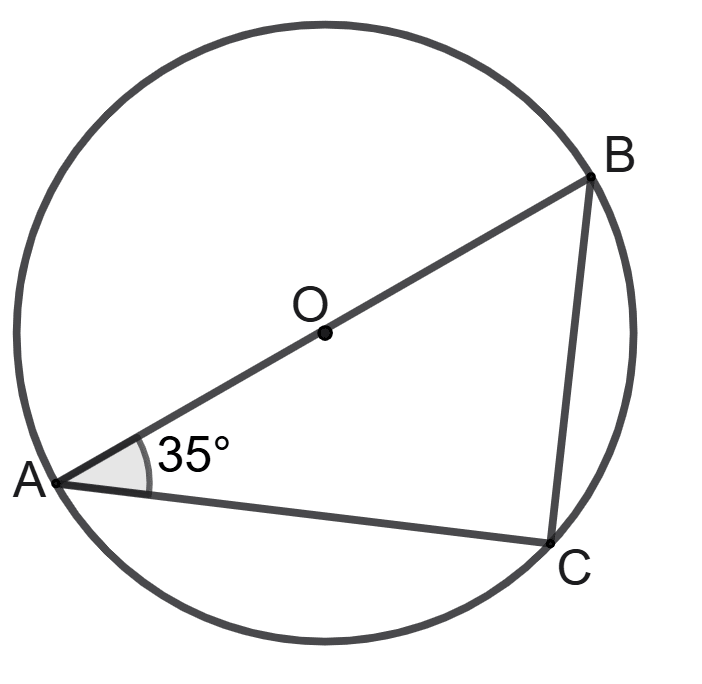
If angle CAB = 35°, find the measure of angle ABC.