Mathematics
The following figure shows a closed victory-stand whose dimensions are given in cm.
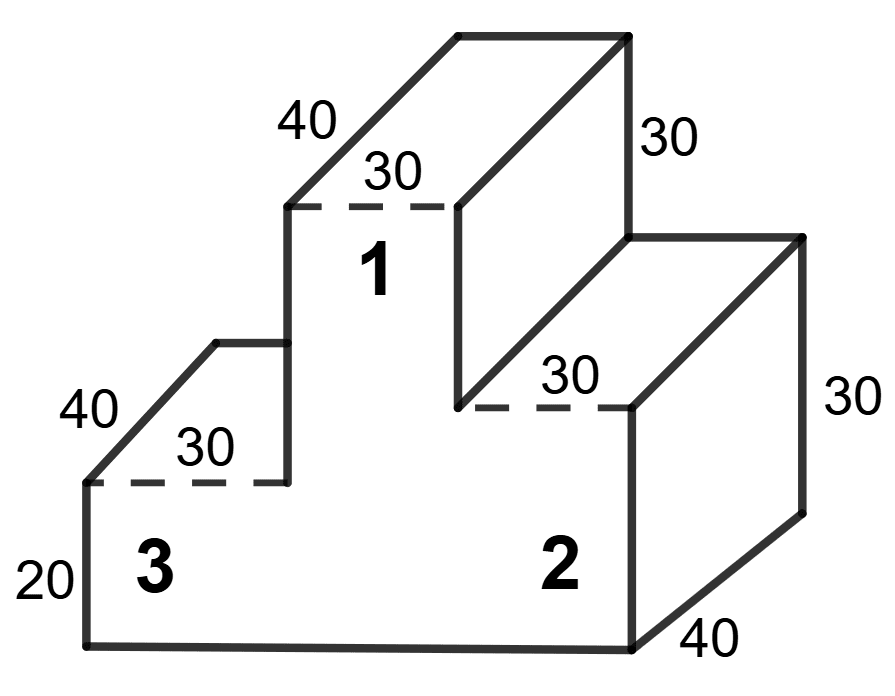
Find the volume and the surface area of the victory stand.
Answer
Given:
The dimensions of step 1 = 30 cm x 40 cm x (30 + 30) cm
The dimensions of step 2 = 40 cm x 30 cm x 30 cm
The dimensions of step 3 = 40 cm x 30 cm x 20 cm
Total volume of victory stand = Volume of step 1 + Volume of step 2 + Volume of step 3
(∵ Volume of cuboid = l x b x h)
Total volume of victory stand = 40 x 30 x 60 + 40 x 30 x 30 + 40 x 30 x 20 cm3
= 72,000 + 36,000 + 24,000 cm3
= 1,32,000 cm3
We know that
Total surface area = Area of front and back + Area of vertical faces + Area of top faces
Putting the values, we get
= 2(30 x 20 + 30 x 60 + 30 x 30) + (20 x 40 + 40 x 40 + 30 x 40 + 30 x 40) + 3(30 x 40) cm2
= 2(600 + 1,800 + 900) + (800 + 1,600 + 1,200 + 1,200) + 3 x 1,200 cm2
= 2 x 3,300 + 4,800 + 3,600 cm2
= 6,600 + 4,800 + 3,600 cm2
= 15,000 cm2
Hence, the volume of the victory stand is 1,32,000 cm3 and the surface area is 15,000 cm2.
Related Questions
A rectangular card-board sheet has length 32 cm and breadth 26 cm. Squares each of side 3 cm, are cut from the corners of the sheet and the sides are folded to make a rectangular container. Find the capacity of the container formed.
A swimming pool is 18 m long and 8 m wide. Its deep and shallow ends are 2 m and 1.2 m respectively. Find the capacity of the pool, assuming that the bottom of the pool slopes uniformly.
Each face of a cube has perimeter equal to 32 cm. Find its surface area and its volume.
A school auditorium is 40 m long, 30 m broad and 12 m high. If each student requires 1.2 m2 of the floor area; find the maximum number of students that can be accommodated in this auditorium. Also, find the volume of air available in the auditorium, for each student.