Mathematics
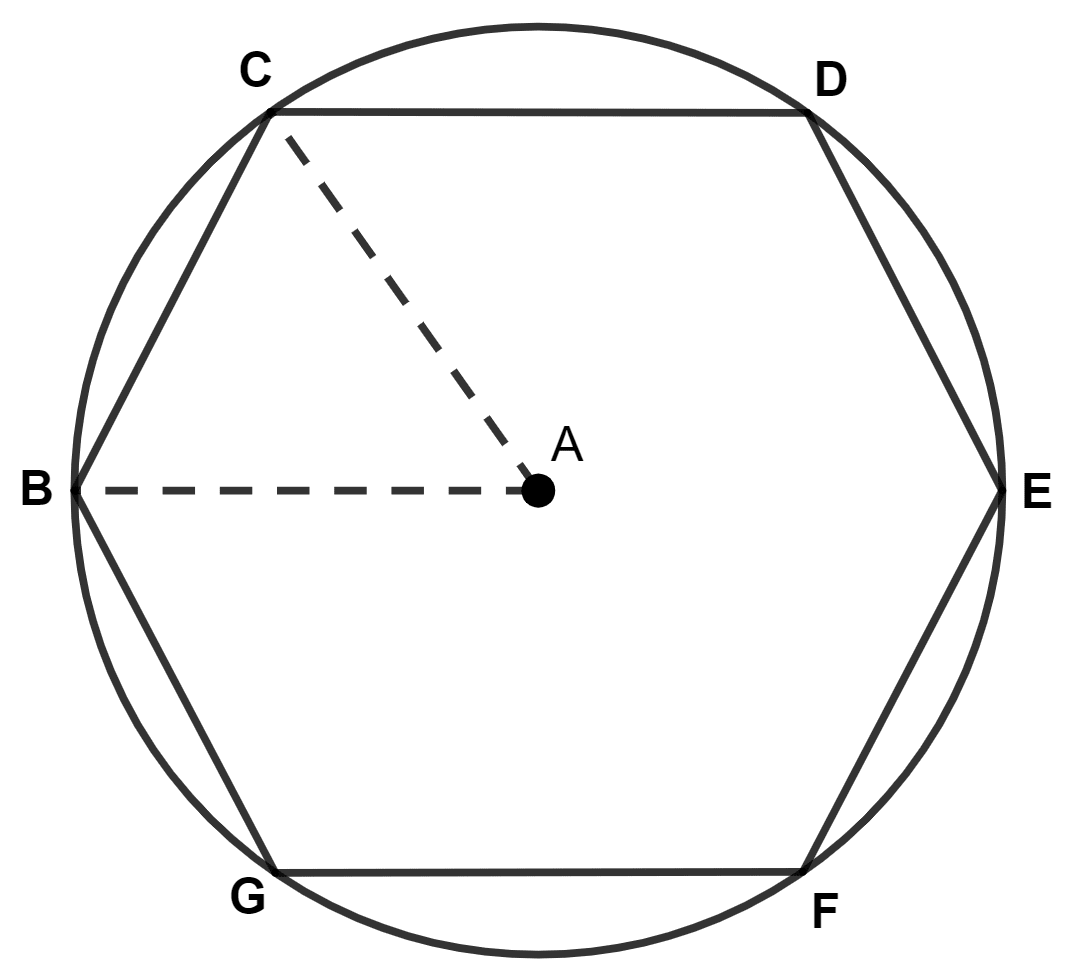
For a regular hexagon inscribed in a circle, the radius of the circle and the length of a side of the hexagon are :
equal
not equal
equal, if hexagon is regular
not equal, if hexagon is regular.
Related Questions
Incenter of a triangle is the point of intersection of the :
perpendicular bisector of its sides
bisectors of its angles
one perpendicular of its side and bisector of any one angle of it
none of these.
For a regular hexagon, inscribing a circle, the length of the side of the hexagon and the radius of the circle are :
equal
not equal
side of hexagon is bigger than the radius of the circle
side of hexagon is smaller than the radius of the circle.
In triangle ABC, bisectors of angles A and B meet at point P.
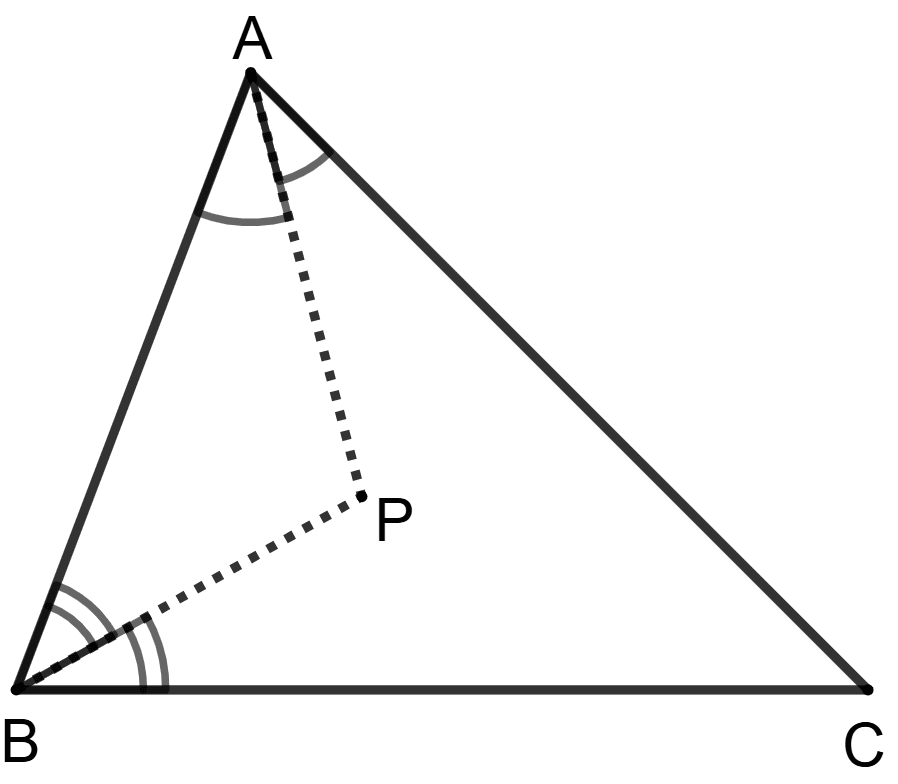
Assertion (A): PC bisects angle C.
Reason(R): Bisectors of angles of a triangle are concurrent.
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.
In triangle ABC, ∠A = 35° and ∠C = 55°.
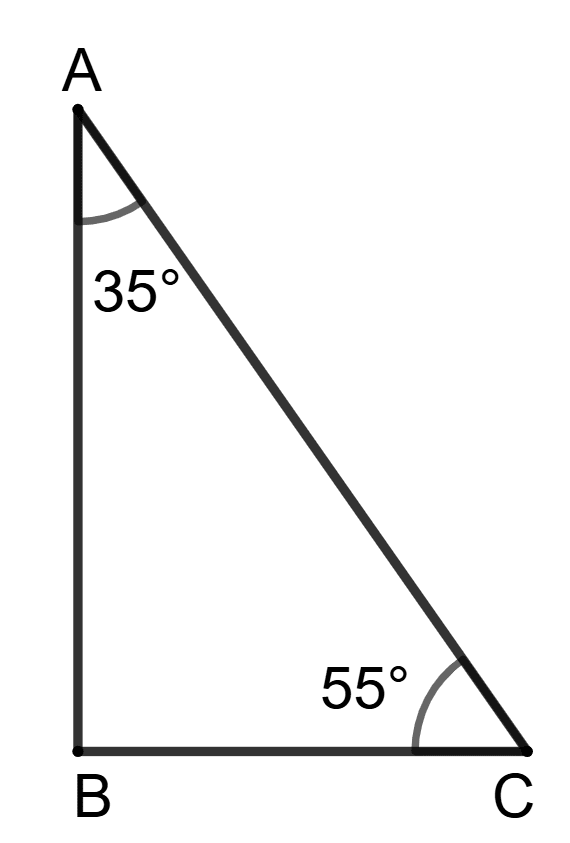
Assertion (A): Circle with AC as diameter will pass through the vertex B.
Reason(R): ∠ABC = 180° - (35° + 55°) = 90° = angle of semi-circle.
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.