Mathematics
For a regular hexagon, inscribing a circle, the length of the side of the hexagon and the radius of the circle are :
equal
not equal
side of hexagon is bigger than the radius of the circle
side of hexagon is smaller than the radius of the circle.
Constructions
9 Likes
Answer
We know that,
A regular hexagon comprises 6 equilateral triangles.

∴ BAC is an equilateral triangle.
∴ AB = BC = CA.
From figure,
⇒ AP < CA
⇒ AP < BC
⇒ Radius < Side of hexagon
Hence, Option 3 is the correct option.
Answered By
5 Likes
Related Questions
In the given figure, AP is bisector of angle A of △ ABC and DP is perpendicular bisector of side AB, then :

P is incenter of △ ABC
P is circumcenter of △ ABC
PB bisects angle B
none of these
Incenter of a triangle is the point of intersection of the :
perpendicular bisector of its sides
bisectors of its angles
one perpendicular of its side and bisector of any one angle of it
none of these.
For a regular hexagon inscribed in a circle, the radius of the circle and the length of a side of the hexagon are :
equal
not equal
equal, if hexagon is regular
not equal, if hexagon is regular.
In triangle ABC, bisectors of angles A and B meet at point P.
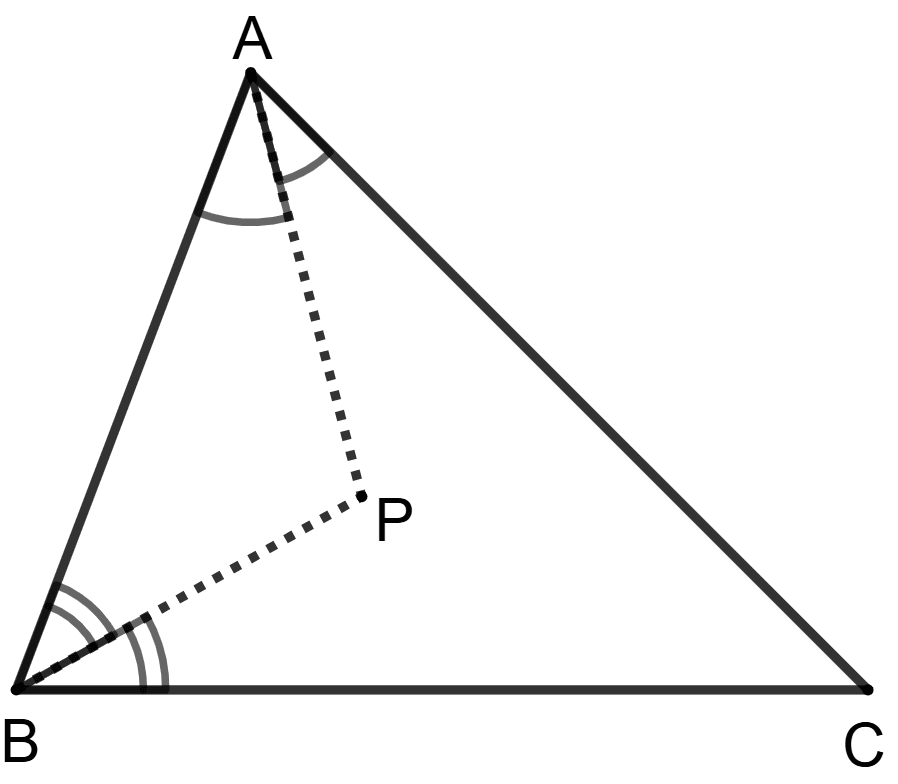
Assertion (A): PC bisects angle C.
Reason(R): Bisectors of angles of a triangle are concurrent.
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.