Mathematics
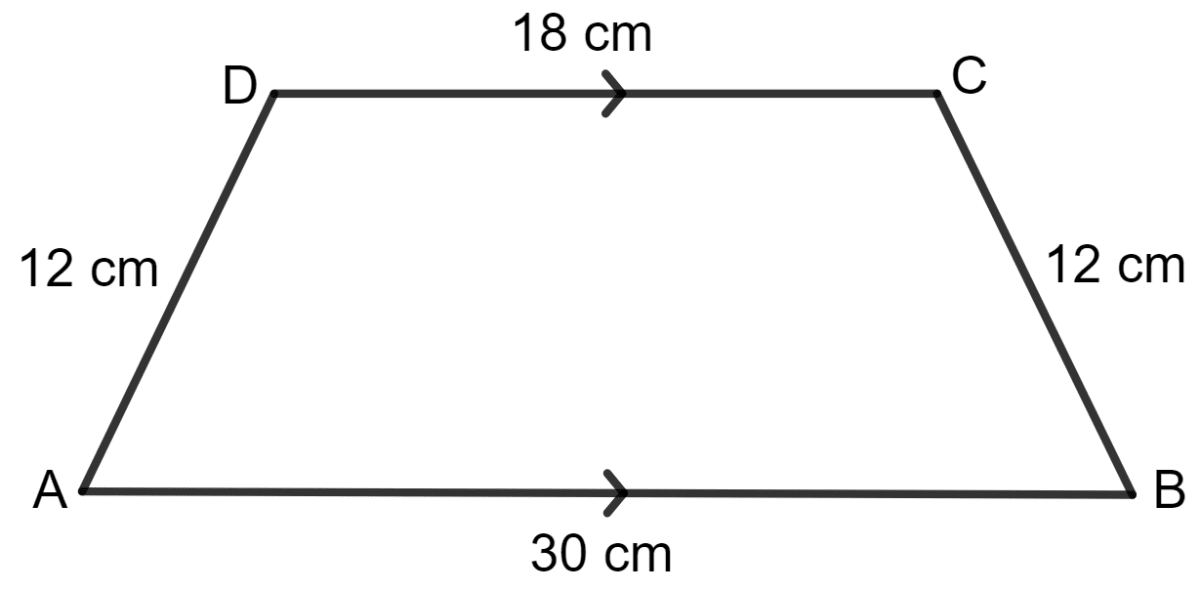
For the trapezium given below; find its area.
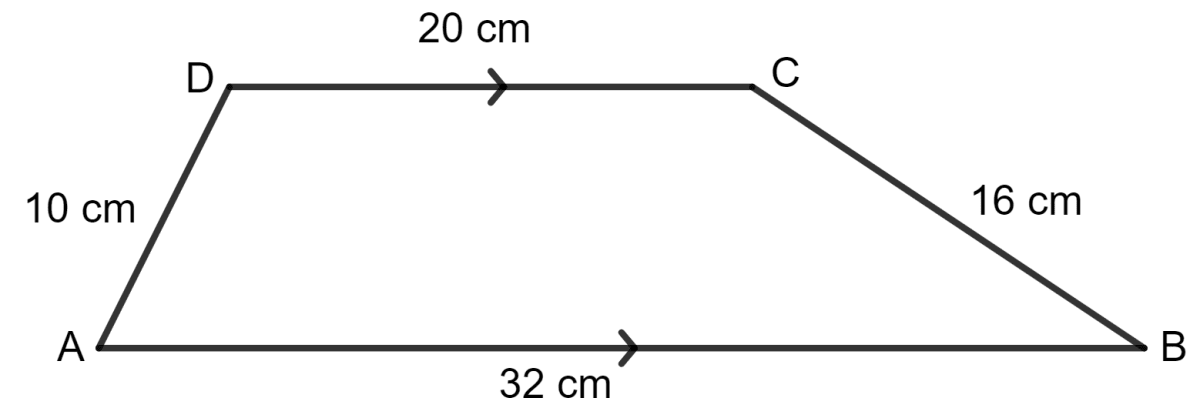
Mensuration
4 Likes
Answer
Draw CE parallel to DA which meets AB at point E.
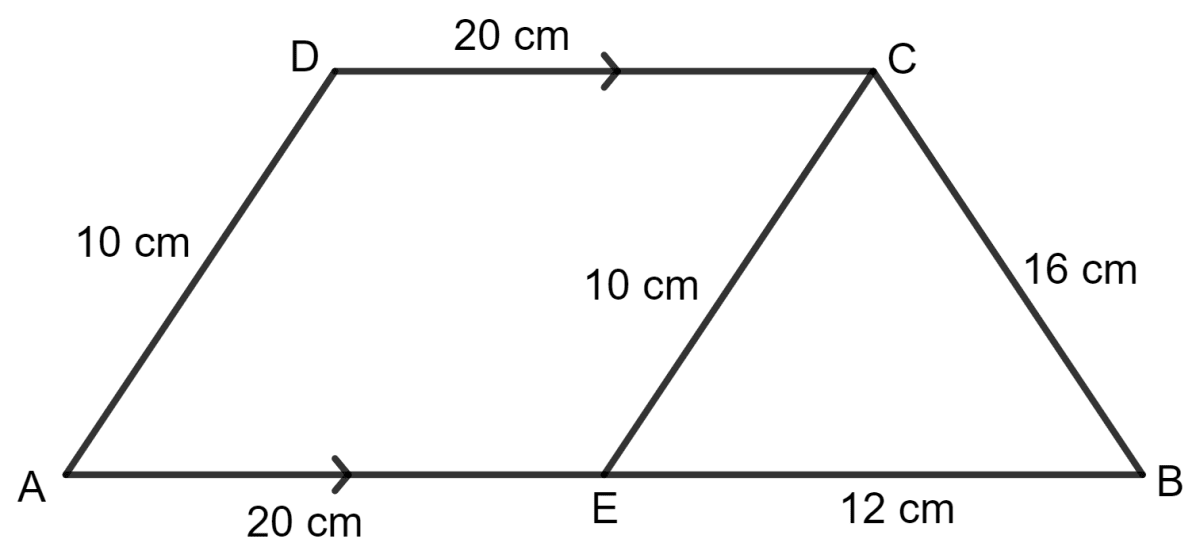
AE = DC = 20 cm
AB = AE + EB
⇒ 32 = 20 + EB
⇒ EB = 32 - 20 = 12 cm
And, DA = CE = 10 cm
For the Δ EBC,
Let the sides of the triangle be:
a = 10 cm, b = 12 cm and c = 16 cm.
The semi-perimeter s:
∵ Area of triangle EBC =
= cm2
= cm2
= cm2
= 59.9 cm2
Let h be the height of Δ EBC,
Area of Δ EBC = x base x height
⇒ x 12 x height = 59.9
⇒ 6 x height = 59.9
⇒ height =
⇒ height = 9.98 cm
Area of trapezium ABCD = x (sum of parallel sides) x height
= x (20 + 32) x 9.98
= x 52 x 9.98 sq. cm
= 26 x 9.98 sq. cm
= 259.65 sq. cm
Hence, the area of trapezium ABCD is 259.65 sq. cm.
Answered By
1 Like
Related Questions
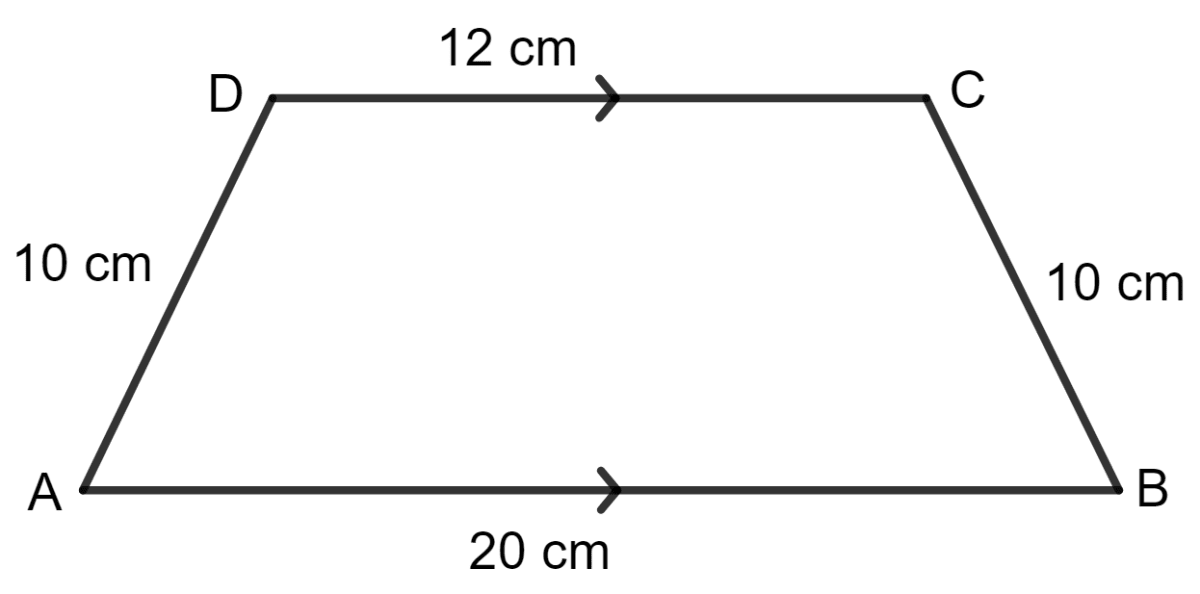
For the trapezium given below; find its area.
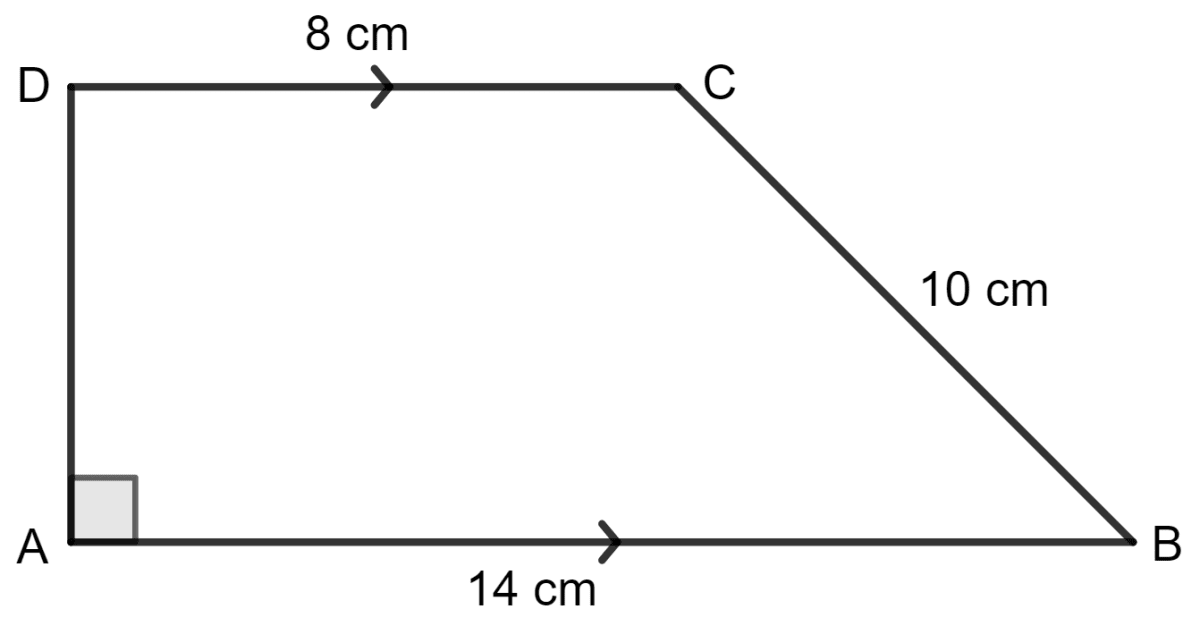
For the trapezium given below; find its area.
For the trapezium given below; find its area.
The perimeter of a rectangular board is 70 cm. Taking its length as x cm, find its width in terms of x.
If the area of the rectangular board is 300 cm2; find its dimensions.