Mathematics
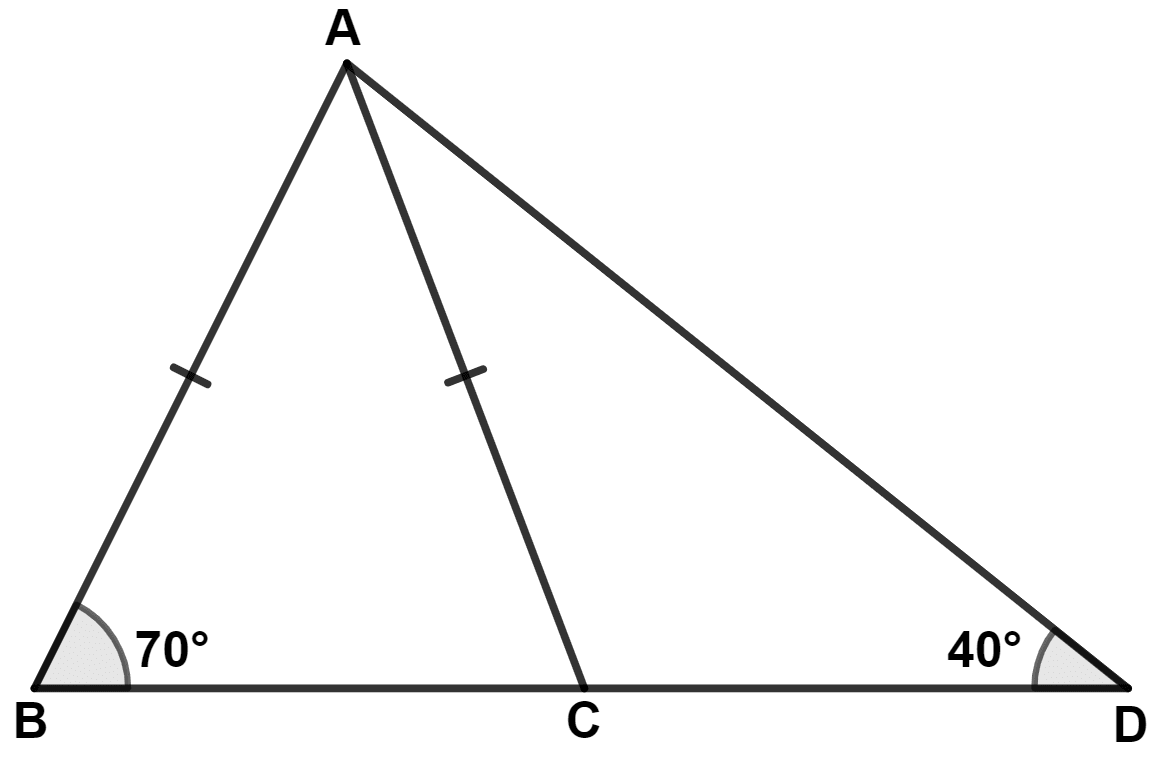
From the following figure, prove that : AB > CD.
Triangles
25 Likes
Answer
In △ ABC,
⇒ AB = AC (Given)
⇒ ∠C = ∠B = 70°
By angle sum property of triangle,
⇒ ∠BAC + ∠B + ∠C = 180°
⇒ ∠BAC + 70° + 70° = 180°
⇒ ∠BAC + 140° = 180°
⇒ ∠BAC = 180° - 140° = 40°.
In △ ABD,
By angle sum property of triangle,
⇒ ∠BAD + ∠B + ∠D = 180°
⇒ ∠BAD + 70° + 40° = 180°
⇒ ∠BAD + 110° = 180°
⇒ ∠BAD = 180° - 110° = 70°.
From figure,
⇒ ∠CAD = ∠BAD - ∠BAC = 70° - 40° = 30°.
In △ ACD,
Since, ∠CDA > ∠CAD
∴ AC > CD (If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.)
Since, AB = AC
∴ AB > CD.
Hence, proved that AB > CD.
Answered By
18 Likes
Related Questions
In the given figure, we find :
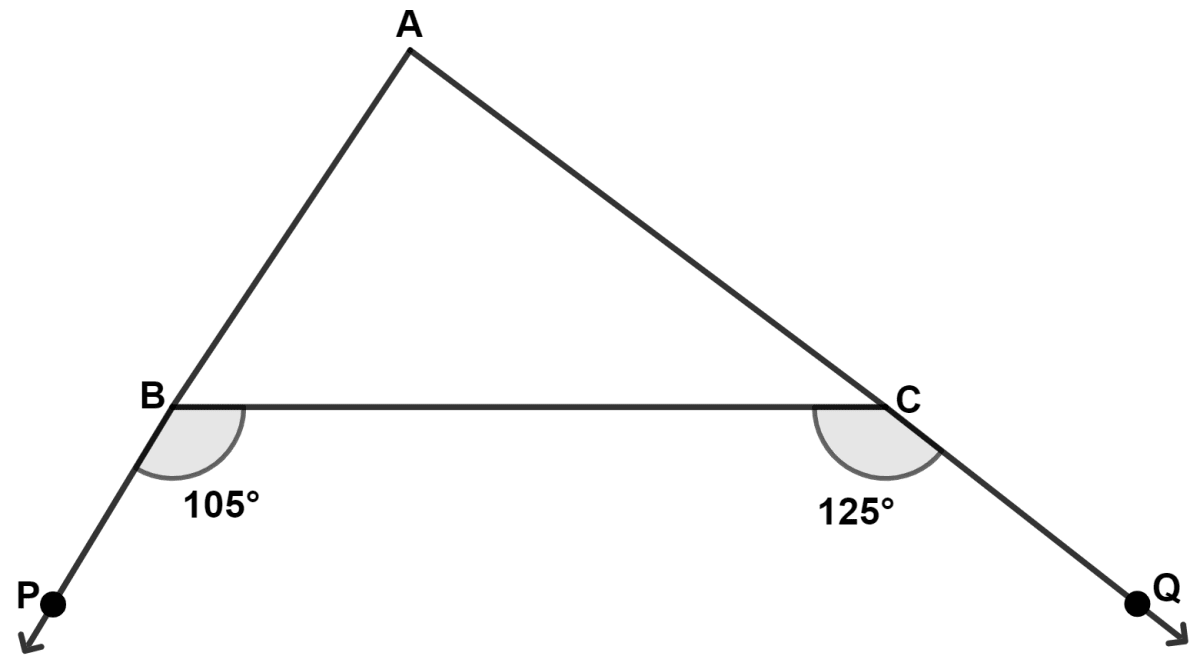
AB > AC
AC > AB
AB < BC
AC = AB
In a quadrilateral ABCD,
AB + BC + CD + DA > AC + BD
AB + BC + CD + DA < AC + BD
AB + BC + CD + DA = AC + BD
AB + BC < AC
In a triangle PQR; QR = PR and ∠P = 36°. Which is the largest side of the triangle ?
If two sides of a triangle are 8 cm and 13 cm, then the length of the third side is between a cm and b cm. Find the values of a and b such that a is less than b.