Mathematics
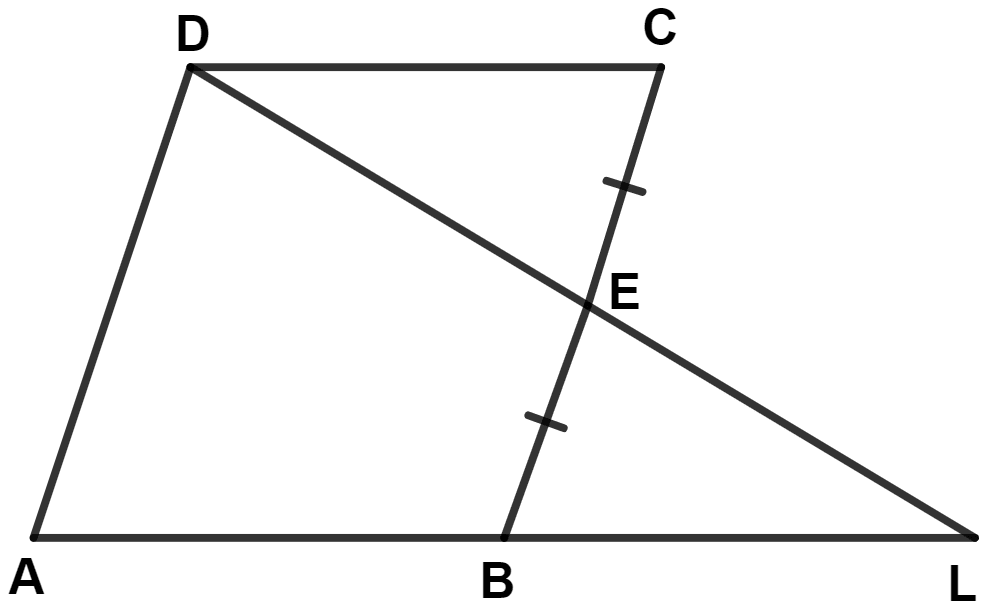
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid point of BC.
Prove that :
(i) △ DCE ≅ △ LBE
(ii) AB = BL
(iii) AL = 2DC
Answer
(i) In parallelogram ABCD,
AB || CD
Since, ABL is a straight line.
∴ BL || CD
In △ LBE and △ DCE,
⇒ BE = CE (Given)
⇒ ∠BEL = ∠CED (Vertically opposite angles are equal)
⇒ ∠CDE = ∠ELB (Alternate angles are equal)
∴ △ LBE ≅ △ DCE (By A.A.S. axiom)
Hence, proved that △ LBE ≅ △ DCE.
(ii) We know that,
Opposite sides of parallelogram are equal.
∴ AB = CD …….(1)
Since, △ LBE ≅ △ DCE
We know that,
Corresponding parts of congruent triangles are equal.
∴ DC = BL …….(2)
From equation (1) and (2), we get :
AB = BL.
Hence, proved that AB = BL.
(iii) Given,
⇒ AB = CD
⇒ AL - BL = CD
⇒ AL - CD = CD (Using Eq 2)
⇒ AL = CD + CD
⇒ AL = 2CD.
Hence, proved that AL = 2CD.
Related Questions
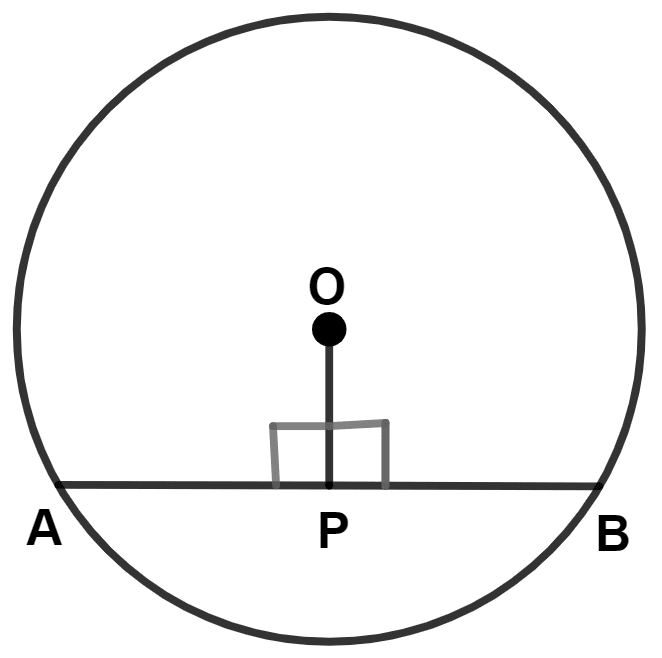
The following figure shows a circle with center O. If OP is perpendicular to AB, prove that AP = BP.
In a triangle ABC, D is mid-point of BC; AD is produced upto E, so that DE = AD. Prove that :
(i) △ ABD and △ ECD are congruent.
(ii) AB = EC
(iii) AB is parallel to EC.
On the sides AB and AC of triangle ABC, equilateral triangles ABD and ACE are drawn. Prove that :
(i) ∠CAD = ∠BAE
(ii) CD = BE.
A line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that : QA = QB.