Mathematics
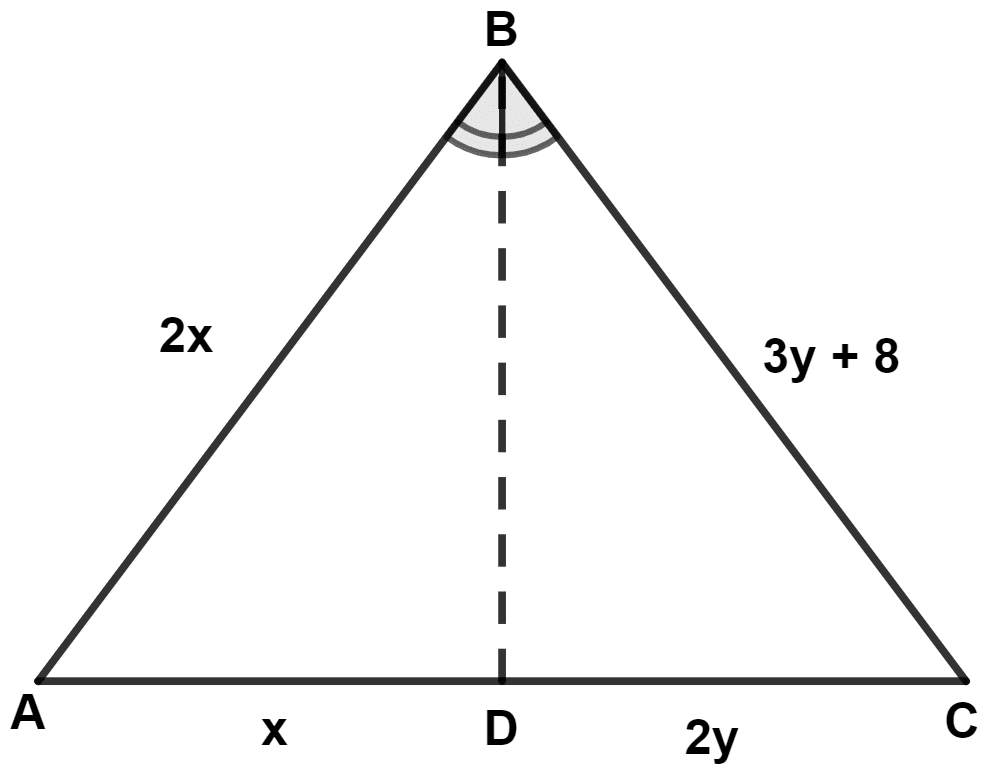
From the given figure, if ∠A = ∠C, we get :
x = 8, y = 16
x = -8, y = 16
x = 16, y = -8
x = 16, y = 8
Triangles
11 Likes
Answer
In △ ABD and △ CBD,
⇒ ∠A = ∠C (Given)
⇒ BD = BD (Common side)
⇒ ∠ABD = ∠CBD (Given)
∴ △ ABD ≅ △ CBD (By A.A.S. axiom)
We know that,
Corresponding sides of congruent triangle are equal.
∴ AB = BC and AD = CD.
Considering AD = CD,
⇒ x = 2y ……(1)
Considering AB = BC,
⇒ 2x = 3y + 8
Substituting value of x from equation (1) in above equation, we get :
⇒ 2(2y) = 3y + 8
⇒ 4y = 3y + 8
⇒ 4y - 3y = 8
⇒ y = 8
⇒ x = 2y = 2(8) = 16.
Hence, Option 4 is the correct option.
Answered By
5 Likes
Related Questions
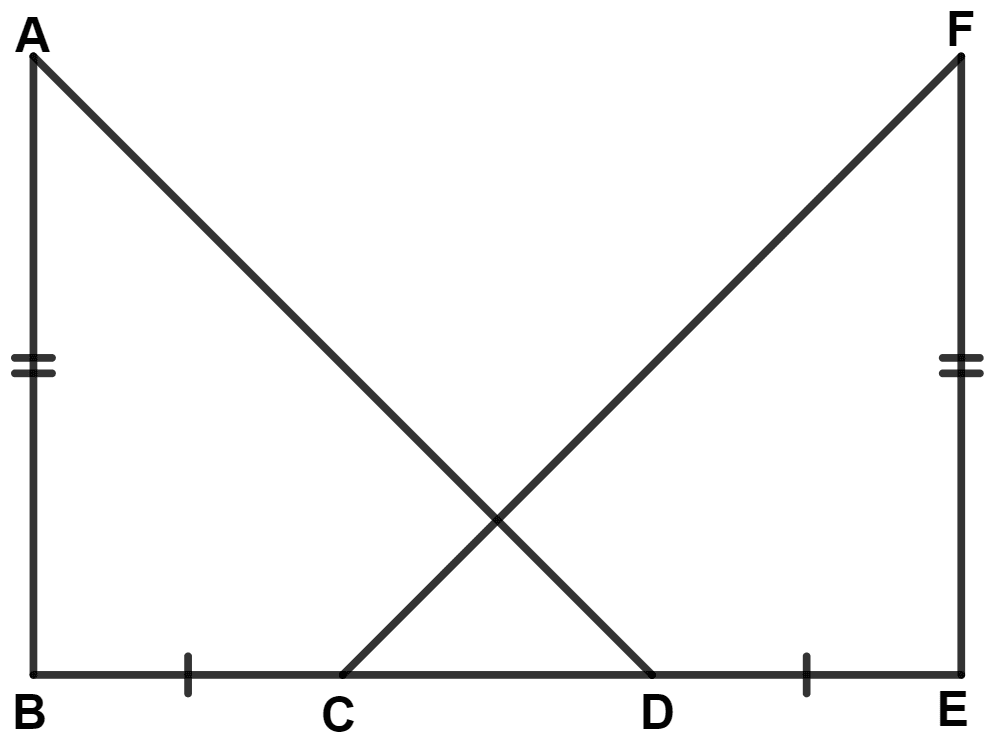
In the given figure, AB ⊥ BE, EF ⊥ BE, AB = EF and BC = DE, then :
△ ABD ≅ △ EFC
△ ABD ≅ △ FEC
△ ABD ≅ △ ECF
△ ABD ≅ △ CEF
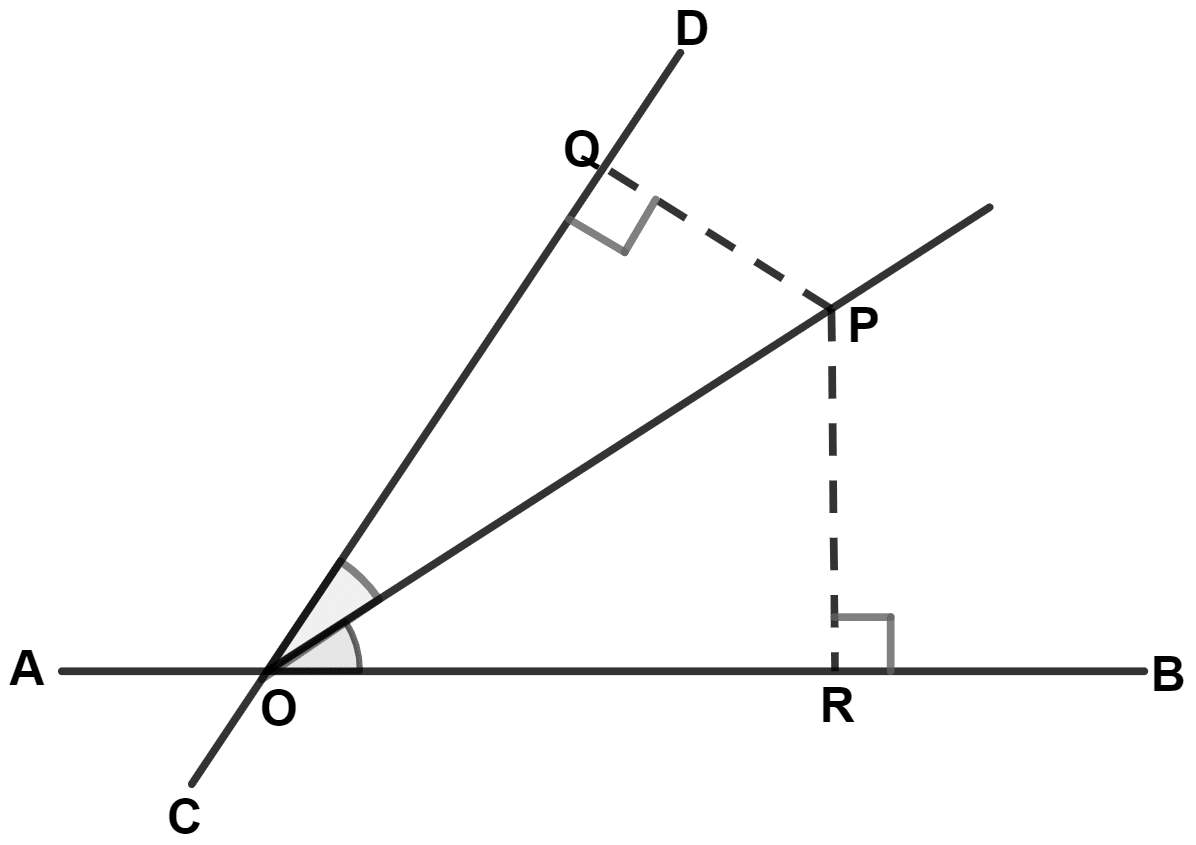
From the adjoining figure, we find :
OP = OR
OP = OQ
PQ = PR
PR ≠ PQ
ABCD is a rectangle. X and Y are points on sides AD and BC respectively such that AX = BY, then :
AY ≠ BX
△ ABX ≅ △ BYA
△ ABX ≅ △ AYB
△ ABX ≅ △ BAY
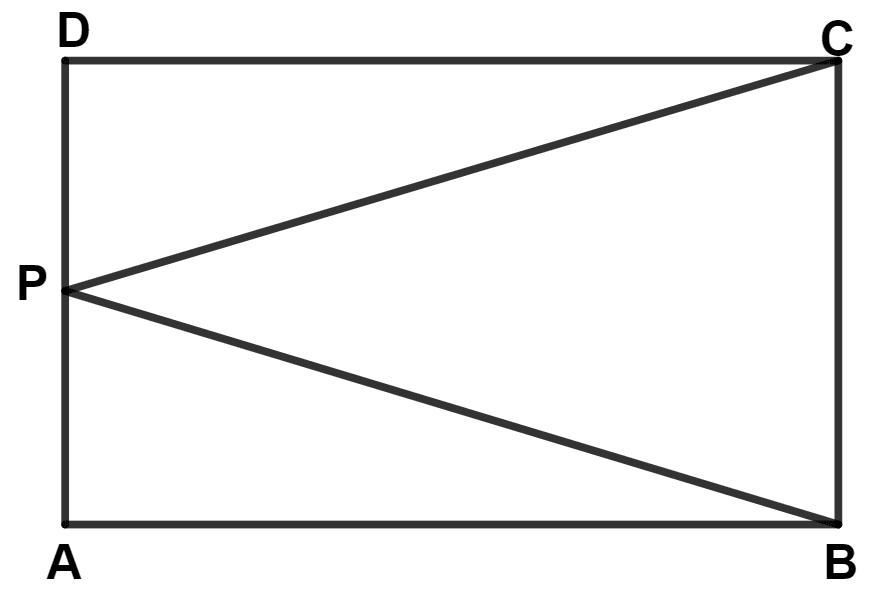
In the given figure, P is mid-point of side AD of rectangle ABCD; then :
∠PBC = ∠PBA
∠PBC = ∠PCB
∠BPA = ∠BPC
∠PBC = ∠BPA