Mathematics
Given A = {x : -1 < x ≤ 5, x ∈ R} and B = {x : -4 ≤ x < 3, x ∈ R}
Represent on different number lines :
(i) A ∩ B
(ii) A' ∩ B
(iii) A - B
Answer
A = {x : -1 < x ≤ 5, x ∈ R} and B = {x : -4 ≤ x < 3, x ∈ R}
(i) A ∩ B = Numbers common to both A and B.
= {x : -1 < x < 3, x ∈ R}
Solution on the number line is :

(ii) A' ∩ B = Numbers which do not belong to A but belong to B
= {x : -4 ≤ x ≤ -1, x ∈ R}
Solution on the number line is :

(iii) A - B = Numbers which belong to A but do not belong to B
= {x : 3 ≤ x ≤ 5}
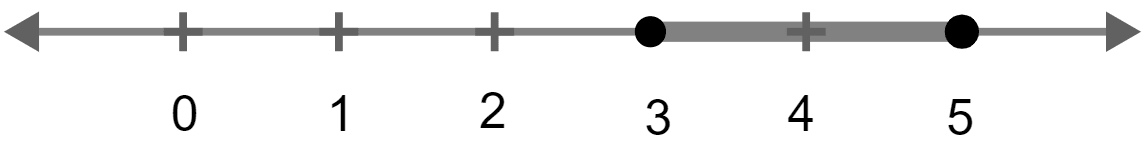
Related Questions
Solve and graph the solution set of :
3x - 2 > 19 or 3 - 2x ≥ -7; x ∈ R
The diagram represents two inequations A and B on a real number lines :

(i) Write down A and B in set builder notation.
(ii) Represent A ∩ B and A ∩ B' on two different number lines.
Given : A = {x : -8 < 5x + 2 ≤ 17, x ∈ I}
B = {x : -2 ≤ 7 + 3x < 17, x ∈ R}
Where R = {real numbers} and I = {integers}
Represent A and B on two different numbers lines. Write down elements of A ∩ B.