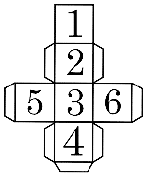
When a die is cast with numbering on its faces, as shown, the ratio of the probability of getting a composite number to the probability of getting a prime number is …………… .

1. 2 : 3

2. 3 : 2

3. 1 : 3

4. 1 : 2

The product of A = $\begin{bmatrix$}[r] 1 & -2 \ -3 & 4 \end{bmatrix} and matrix M, AM = B where B = $\begin{bmatrix$}[r] 2 \ 24 \end{bmatrix}, then the order of matrix M is …………… .

1. 2 × 2

2. 2 × 1

3. 1 × 2

4. 4 × 1

Locus of a moving point is …………… if it moves such that it keeps a fixed distance from a fixed point.

1. Circle

2. Line

3. Angle

4. Line segment

The point of concurrence of the angle bisectors of a triangle is called the …………… of the triangle.

1. centroid

2. incenter

3. circumcenter

4. orthocenter