Mathematics
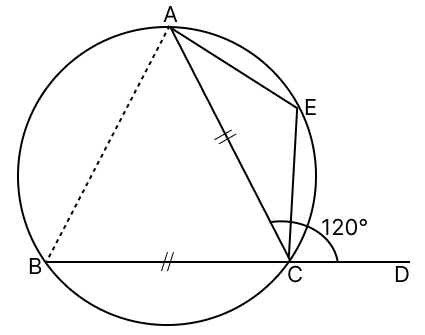
In the given diagram, chords AC and BC are equal. If ∠ACD = 120°, then ∠AEC is:
30°
60°
90°
120°
Circles
20 Likes
Answer
From figure,
∠ACD and ∠ACB forms linear pairs [BD is a straight line].
⇒ ∠ACD + ∠ACB = 180°
⇒ 120° + ∠ACB = 180°
⇒ ∠ACB = 180° - 120°
⇒ ∠ACB = 60°.
In ΔABC,
⇒ BC = AC [Given]
⇒ ∠ABC = ∠BAC = x° (let) [Angles opposite to equal sides in triangle are equal]
According to angle sum property in ΔABC,
⇒ ∠ACB + ∠ABC + ∠BAC = 180°
⇒ 60° + x° + x° = 180°
⇒ 2x° = 180° - 60°
⇒ 2x° = 120°
⇒ x° = = 60°.
From figure,
ABCE is cyclic quadrilateral.
We know that,
Opposite angles of cyclic quadrilateral are supplementary.
⇒ ∠ABC + ∠AEC = 180°
⇒ 60° + ∠AEC = 180°
⇒ ∠AEC = 180° - 60°
⇒ ∠AEC = 120°.
Hence, option 4 is the correct option.
Answered By
9 Likes
Related Questions
The equation of the line passing through origin and parallel to the line 3x + 4y + 7 = 0 is:
3x + 4y + 5 = 0
4x - 3y - 5 = 0
4x - 3y = 0
3x + 4y = 0
If , then A2 is equal to:
The factor common to the two polynomials x2 - 4 and x3 - x2 - 4x + 4
(x + 1)
(x - 1)
(x - 2)
(x - 4)
A man invested in a company paying 12% dividend on its share. If the percentage return on his investment is 10%, then the shares are:
at par
below par
above par
cannot be determined