Mathematics
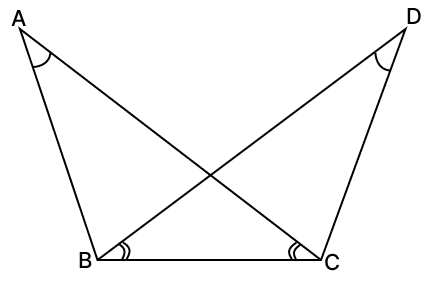
In the given figure, the line segments AB and CD intersect at a point M in such a way that AM = MD and CM = MB. Prove that, AC = BD but AC may not be parallel to BD.
Triangles
1 Like
Answer
In △MAC and △MDB,
⇒ AM = MD [Given]
⇒ CM = MB [Given]
⇒ ∠AMC = ∠DMB [Vertically opposite angles are equal]
∴ △MAC ≅ △MDB (By S.A.S axiom)
⇒ AC = BD [Corresponding parts of congruent triangles are equal.]
⇒ ∠MDB = ∠MAC [Corresponding parts of congruent triangles are equal.]
∴ ∠MDB ≠ ∠MCA
Thus, we cannot prove that AC // BD.
Hence, proved that AC = BD but AC may not be parallel to BD.
Answered By
3 Likes
Related Questions
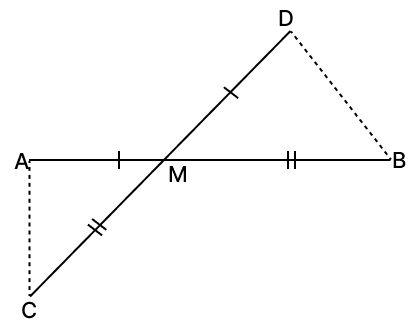
AB is a line segment. AX and BY are two equal line segments drawn on opposite sides of AB such that AX || YB. If AB and XY intersect at M, prove that :
(i) △AMX ≅ △BMY
(ii) AB and XY bisect each other at M.
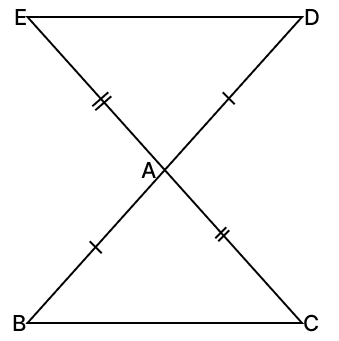
In the given figure, the sides BA and CA of △ABC have been produced to D and E such that BA = AD and CA = AE. Prove that, ED || BC.
If two altitudes of a triangle are equal, prove that it is an isosceles triangle.
In the given figure, ∠BAC = ∠CDB and ∠BCA = ∠CBD. Prove that AB = CD.