Mathematics
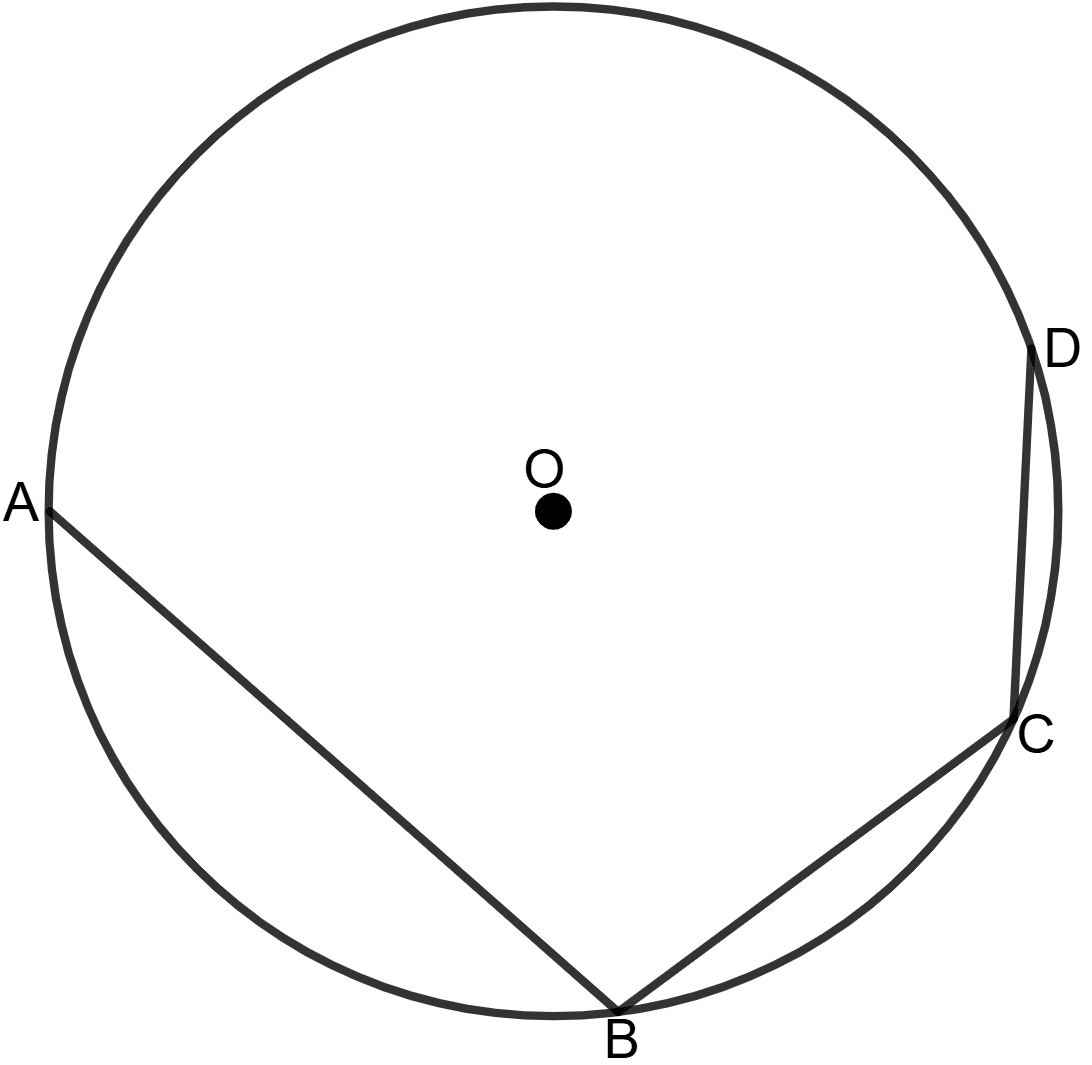
In the given figure, O is the centre of the given circle. AB is a side of a square, BC is a side of regular pentagon and CD is a side of regular hexagon. Find :
(i) ∠AOB
(ii) ∠AOC
(iii) ∠AOD
(iv) ∠BCD
Circles
3 Likes
Answer
Given:
- AB is a side of a square (4 sides).
- BC is a side of a regular pentagon (5 sides).
- CD is a side of a regular hexagon (6 sides).
- O is the centre of the circle.
Construction: Join OA, OB, OC and OD.
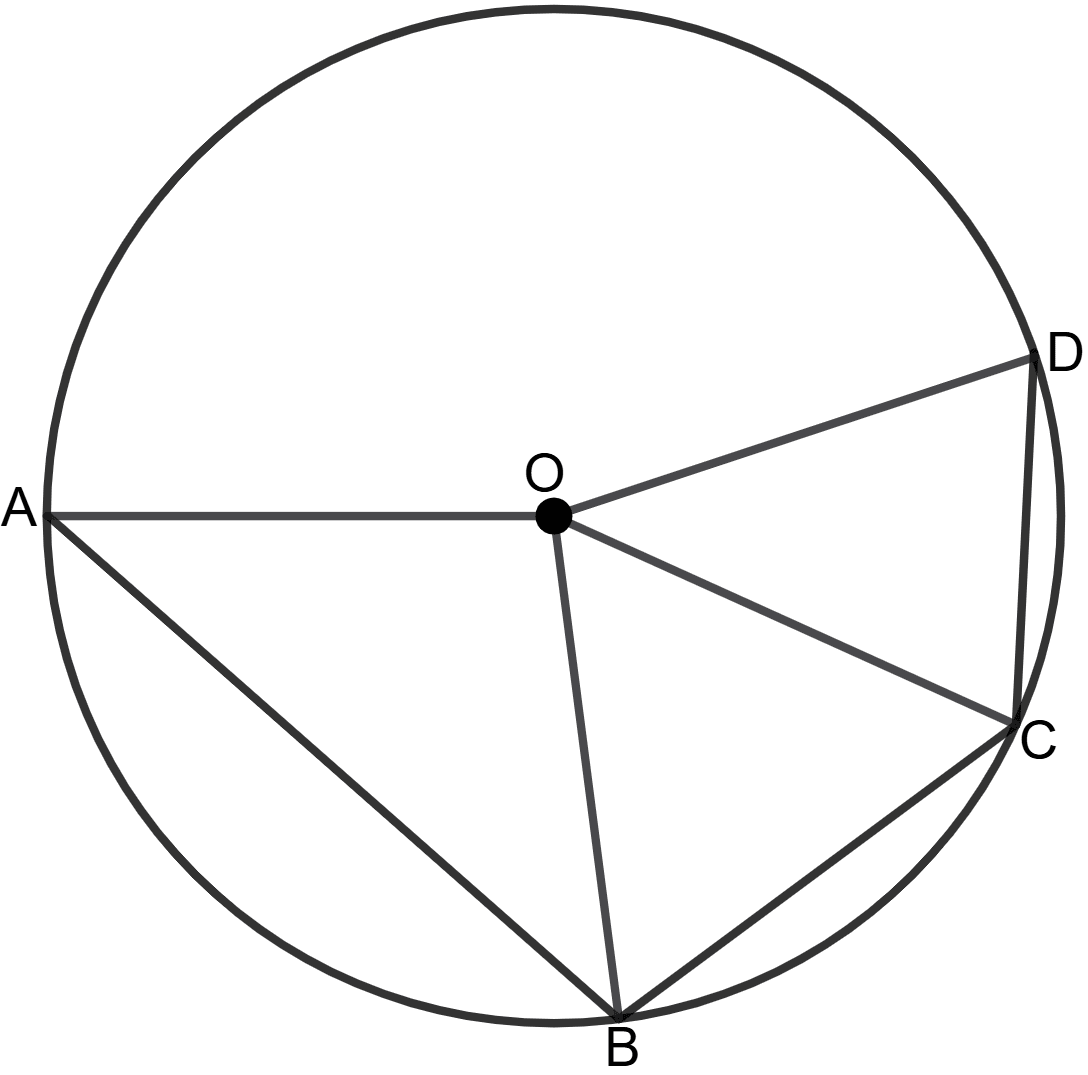
(i) Since AB is a side of a square inscribed in a circle, the angle subtended at the centre is:
∠AOB =
= 90°
Hence, ∠AOB = 90°.
(ii) BC is a side of a regular pentagon, so:
∠BOC =
= 72°
∠AOC = ∠AOB + ∠BOC = 90° + 72° = 162°
Hence, ∠AOC = 162°.
(iii) CD is a side of a regular hexagon, so:
∠COD =
= 60°
∠AOD = ∠AOB + ∠BOC + ∠COD = 90° + 72° + 60° = 222°
Hence, ∠AOD = 222°.
(iv) In Δ BOC,
- OB = OC (radii of same circle)
- ∠BOC = 72°
Using the angle sum property:
∠BOC + ∠BCO + ∠CBO = 180°
⇒ 72° + ∠OBC + ∠OBC = 180°
⇒ 72° + 2∠OBC = 180°
⇒ 2∠OBC = 180° - 72°
⇒ 2∠OBC = 108°
⇒ ∠OBC =
⇒ ∠OBC = 54°
Similarly, in Δ COD,
- OC = OD (radii of same circle)
- ∠COD = 60°
⇒ ∠DOC + ∠OCD + ∠CDO = 180°
⇒ 60° + ∠OCD + ∠OCD = 180°
⇒ 60° + 2∠OCD = 180°
⇒ 2∠OCD = 180° - 60°
⇒ 2∠OCD = 120°
⇒ ∠OCD =
⇒ ∠OCD = 60°
Now, ∠BCD = ∠OBC + ∠OCD
= 54° + 60° = 114°
Hence, ∠BCD = 114°.
Answered By
1 Like
Related Questions
In the given circle, arc APB and arc BQC are in the ratio 2 : 5 and O is centre of the circle.
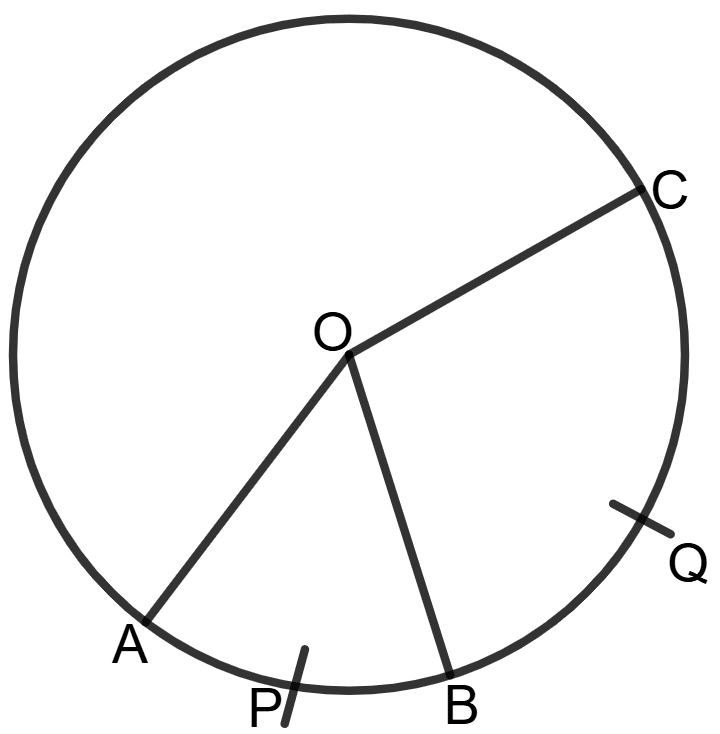
If angle AOB = 44°; find angle AOC.
The given figure shows two congruent circles with centres P and Q. R is mid-point of PQ and ABRCD is a straight line.
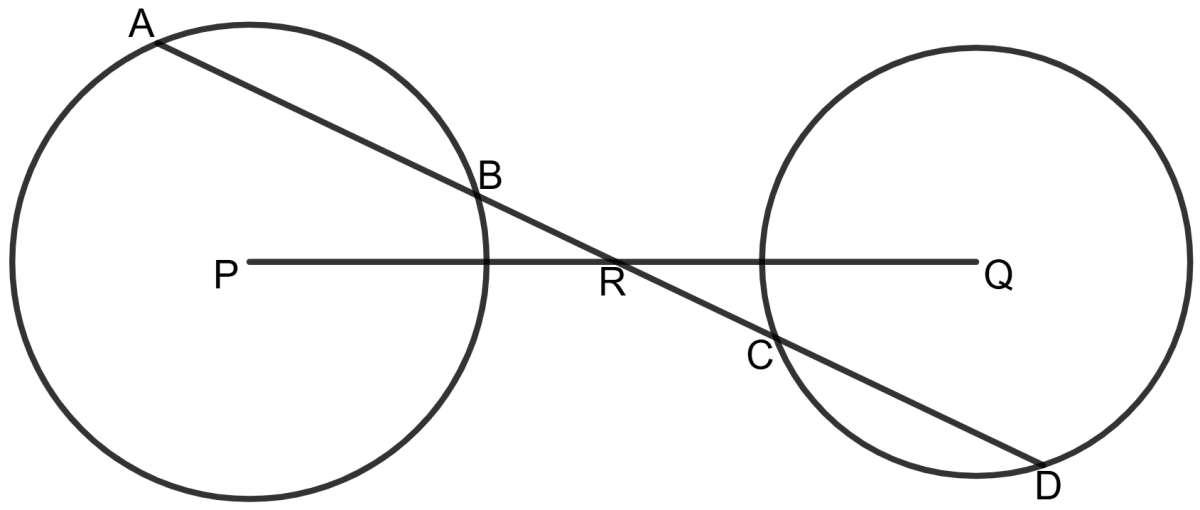
Prove that : AB = CD.
Construct a cumulative frequency distribution table from the following frequency table :
C.I. Frequency 0-12 12 12-24 16 24-36 15 36-48 10 48-60 18 Construct a frequency table from the following cumulative frequency table :
Class interval Cumulative frequency 1-10 7 11-20 15 21-30 30 31-40 42 41-50 60 51-60 75