Mathematics
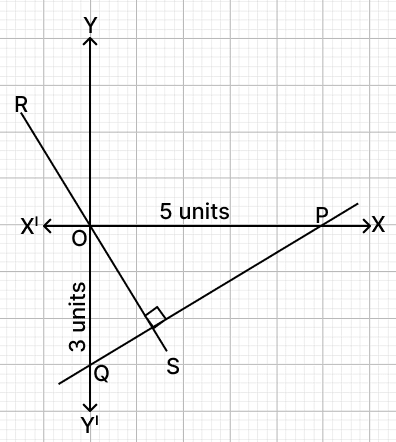
In the given graph, P and Q are points such that PQ cuts off intercepts of 5 units and 3 units along the x-axis and y-axis respectively. Line RS is perpendicular to PQ and passes through the origin. Find the:
(a) coordinates of P and Q
(b) equation of line RS
Straight Line Eq
15 Likes
Answer
(a) Given,
PQ cuts off intercepts of 5 units and 3 units along the x-axis and y-axis respectively.
Thus,
Coordinates of P = (5, 0) and coordinates of Q = (0, -3).
Hence, coordinates of P = (5, 0) and coordinates of Q = (0, -3).
(b) By formula,
Slope (m) =
⇒ Slope of PQ = mPQ = .
We know that,
Product of slopes of perpendicular lines = -1.
⇒ Slope of RS × Slope of PQ = -1
⇒ Slope of RS × = -1
⇒ Slope of RS = .
By point-slope formula,
Equation of line :
Since, slope of RS = and it passes through the origin.
Equation of RS :
⇒
⇒ y =
⇒ 3y = -5x
⇒ 5x + 3y = 0.
Hence, the equation of line RS is 5x + 3y = 0.
Answered By
8 Likes
Related Questions
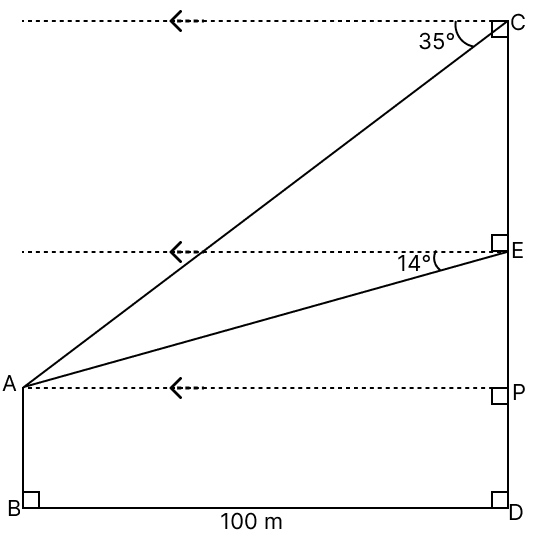
In the given diagram, AB is a vertical tower 100 m away from the foot of a 30 storied building CD. The angles of depression from the point C and E, (E being the mid-point of CD), are 35° and 14° respectively. (Use mathematical table for the required values rounded off correct to two places of decimals only.)
Find the height of the:
(a) tower AB
(b) building CD
Use a graph paper for this question. (Take 2 cm = 10 Marks along one axis and 2 cm = 10 students along another axis). Draw a Histogram for the following distribution which gives the marks obtained by 164 students in a particular class and hence find the Mode.
Marks Number of students 30 - 40 10 40 - 50 26 50 - 60 40 60 - 70 54 70 - 80 34 Refer to the given bill. A customer paid ₹2,000 (rounded off to the nearest ₹10) to clear the bill.
Note: 5% discount is applicable on an article if 10 or more such articles are purchased.
Article M.P.(₹) Quantity G.S.T A 190 06 12% B 50 12 18% Check whether the total amount paid by the customer is correct or not. Justify your answer with necessary working.
A man bought ₹200 shares of a company at 25% premium. If he received a return of 5% on his investment. Find the :
(a) market value
(b) dividend percent declared
(c) number of shares purchased, if annual dividend is ₹1,000.