Mathematics
The given graph represents the monthly salaries (in ₹) of workers of a factory.
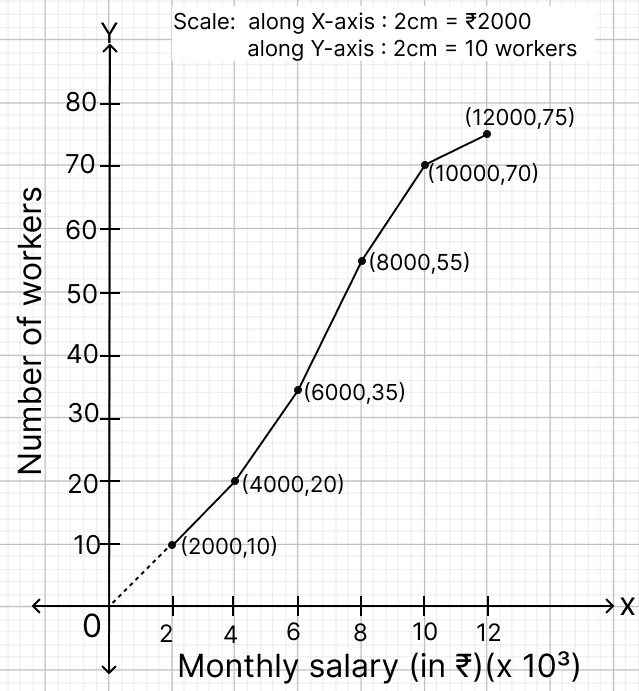
Using graph answer the following:
(a) the total number of workers.
(b) the median class.
(c) the lower-quartile class.
(d) number of workers having monthly salary more than or equal to ₹6,000 but less than ₹10,000.
Measures of Central Tendency
18 Likes
Answer
| Monthly salary | cf |
|---|---|
| 0-2000 | 10 |
| 2000 - 4000 | 20 |
| 4000 - 6000 | 35 |
| 6000 - 8000 | 55 |
| 8000 - 10000 | 70 |
| 10000 - 12000 | 75 |
(a) From the graph, the cumulative frequency at ₹12,000 is 75.
Hence, the total number of workers = 75.
(b) By formula,
Median =
Total workers = 75
From table,
36 to 55 worker lies in the class 6000 - 8000.
Thus, 38th worker lies in the class 6000 - 8000.
Hence, the median class = 6000 – 8000.
(c) Lower quartile =
From table,
11 to 20 worker lies in the class 2000 - 4000.
Thus, 19th worker lies in the class 2000 - 4000.
Hence, the lower-quartile class = 2000 – 4000.
(d) From table,
Number of workers having salary less than ₹ 10,000 = 70
Number of workers having salary less than ₹ 6,000 = 35
Number of workers in this range = 70 − 35 = 35 workers.
Hence, the number of workers having monthly salary more than or equal to ₹ 6,000 but less than ₹ 10,000 = 35.
Answered By
9 Likes
Related Questions
Ms. Sushmita went to a fair and participated in a game. The game consisted of a box having number cards with numbers from 01 to 30. The three prizes were as per the given table:
Prize Number on the card drawn at random is a Wall clock perfect square Water bottle even number which is also a multiple of 3 Purse prime number Find the probability of winning a:
(a) Wall Clock
(b) Water Bottle
(c) Purse
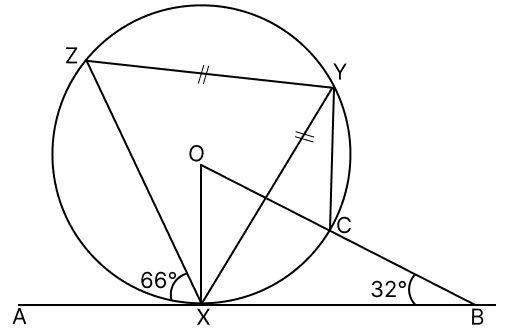
X, Y, Z and C are the points on the circumference of a circle with centre O. AB is a tangent to the circle at X and ZY = XY. Given ∠OBX = 32° and ∠AXZ = 66°. Find:
(a) ∠BOX
(b) ∠CYX
(c) ∠ZYX
(d) ∠OXY
If 1701 is the nth term of the Geometric Progression (G.P.) 7, 21, 63……, find :
(a) the value of 'n'
(b) hence find the sum of the 'n' terms of the G.P.
In the given diagram O is the centre of the circle. Chord SR produced meets the tangent XTP at P.
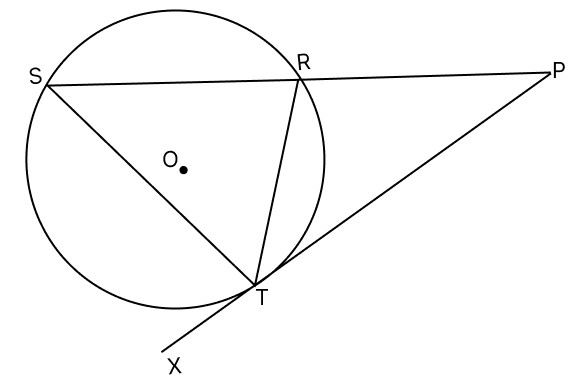
(a) Prove that ΔPTR ~ ΔPST
(b) Prove that PT2 = PR × PS
(c) If PR = 4 cm and PS = 16 cm, find the length of the tangent PT.