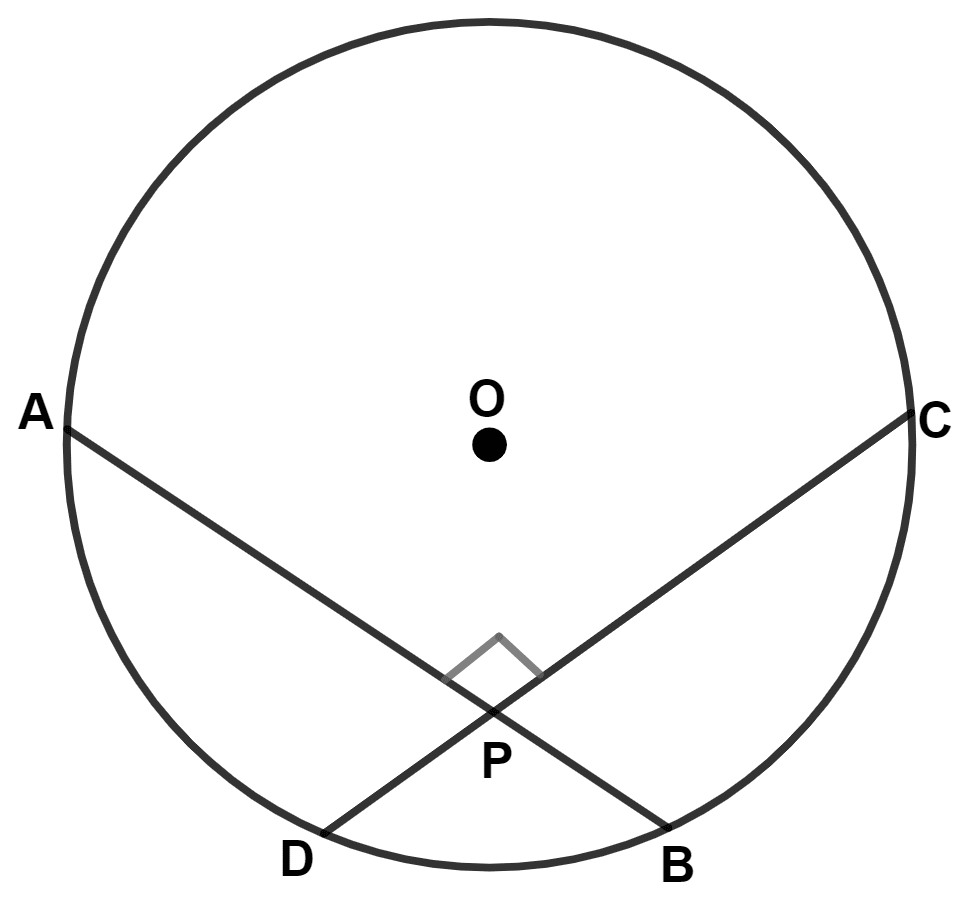
Given two equal chords AB and CD of a circle, with center O, intersecting each other at point P. Prove that :

(i) AP = CP

(ii) BP = DP

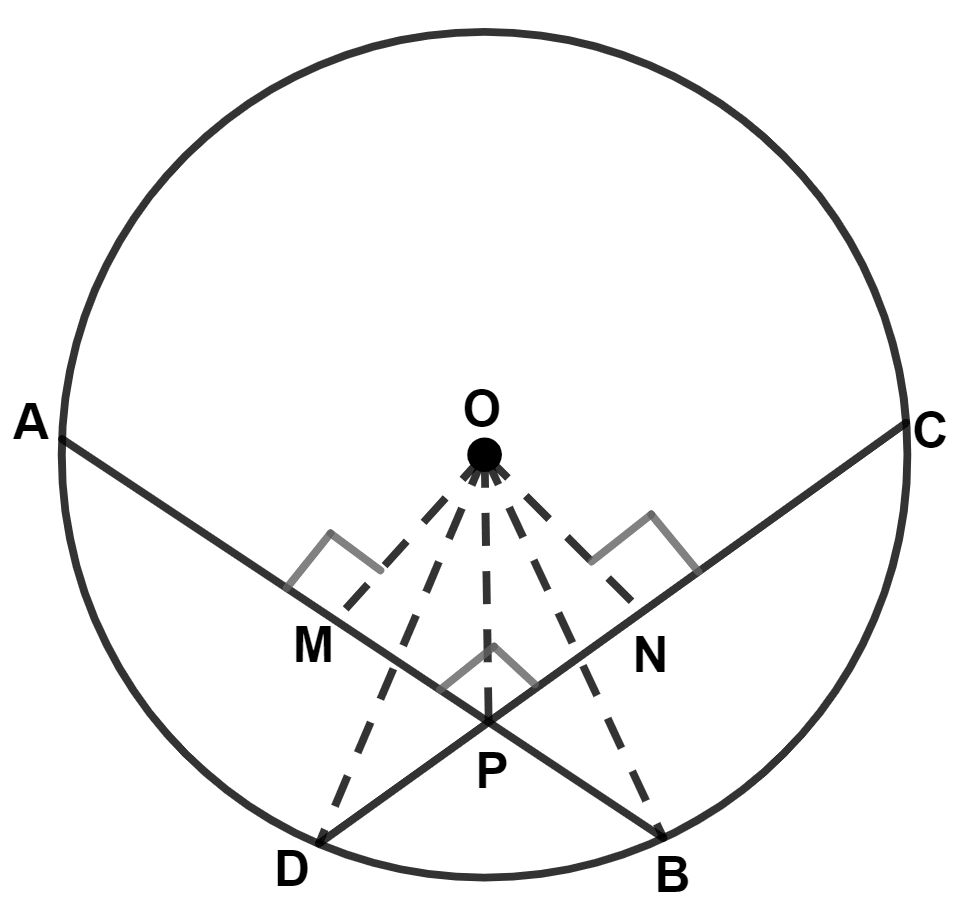
Draw, OM ⊥ AB and ON ⊥ CD.

Join OP, OB and OD.

We know that,

Perpendicular to a chord, from the center of the circle, bisects the chord.

∴ OM and ON bisects AB and CD respectively.

Given,

Two chords are equal.

∴ AB = CD = x (let)

∴ MB = $\dfrac{1}{2}AB = \dfrac{1}{2}x$ and ND = $\dfrac{1}{2}CD = \dfrac{1}{2}x$,

∴ MB = ND …………..(1)

Let, MB = ND = x.

From figure,

OB = OD = y (Radius of same circle)

In right-angled triangle OMB,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OB² = OM² + MB²

⇒ OM² = OB² - MB²

⇒ OM² = y² - x²

⇒ OM = $\sqrt{y^2 - x^2}$ ……..(2)

In right-angled triangle OND,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OD² = ON² + ND²

⇒ ON² = OD² - ND²

⇒ ON² = y² - x²

⇒ ON = $\sqrt{y^2 - x^2}$ ……..(3)

From equation (2) and (3), we get :

⇒ OM = ON

In △ OPM and △ OPN,

⇒ ∠OMP = ∠ONP (Both equal to 90°)

⇒ OP = OP (Common side)

⇒ OM = ON (Proved above)

∴ △ OPM ≅ △ OPN (By R.H.S. axiom)

We know that,

Corresponding parts of congruent triangles are equal.

∴ PM = PN ……….(2)

Subtracting equation (2) from (1), we get :

⇒ MB - PM = ND - PN

⇒ PB = PD ………..(4)

Given,

⇒ AB = CD ………(5)

Subtracting equation (4) from (5), we get :

⇒ AB - PB = CD - PD

⇒ AP = CP.

Hence, proved that AP = CP and BP = DP.