Mathematics
Given two points P and Q, and that (1) the image of P on reflection in y-axis is the point Q and (2) the mid point of PQ is invariant on reflection in x-axis. Locate (i) the x-axis (ii) the y-axis and (iii) the origin.
Reflection
58 Likes
Answer
Given, Q is the image of P on reflection in y-axis and midpoint of PQ is invariant on reflection in x-axis.
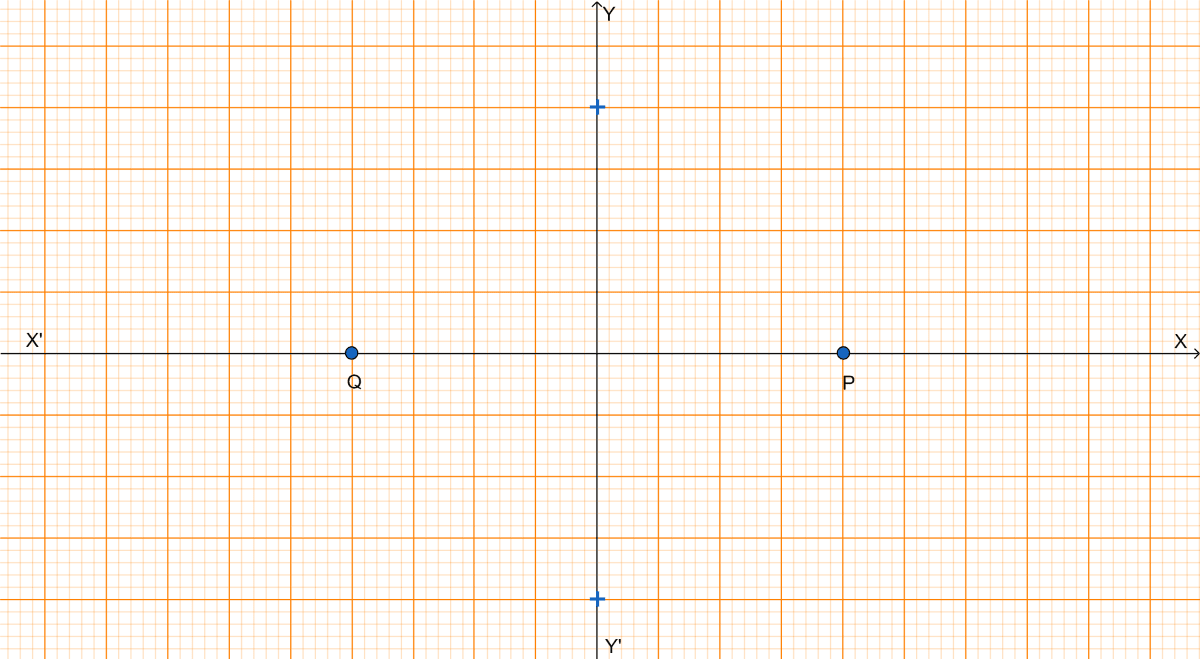
From graph we get,
(i) x-axis will be the line joining the points P and Q.
(ii) The line perpendicular bisector of the line segment PQ is the y-axis.
(iii) The origin will be the mid point of the line segment PQ.
Answered By
35 Likes
Related Questions
The triangle ABC where A(1, 2), B(4, 8), C(6, 8) is reflected in the x-axis to triangle A'B'C'. The triangle A'B'C' is then reflected in the origin to the triangle A''B''C''. Write down the coordinates of A'', B'', C''. Write down a single transformation that maps ABC onto A''B''C''.
The image of a point P on reflection in a line l is a point P'. Describe the location of the line l.
The point (-3, 0) on reflection in a line is mapped as (3, 0) and the point (2, -3) on reflection in the same line is mapped as (-2, -3).
(i) Name the mirror line.
(ii) Write the coordinates of the image of (-3, -4) in the mirror line.
Use graph paper for this question.
Take 2 cm = 1 unit on both the axes.
(i) Plot the points A(0, 4), B(2, 2), C(5, 2) and D(4, 0), E(0, 0) is the origin.
(ii) Reflect B, C, D on the y-axis and name them as B', C' and D' respectively.
(iii) Join the points ABCDD'B'C' and A in order and give a geometrical name to the closed figure.